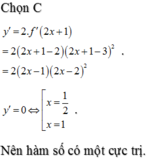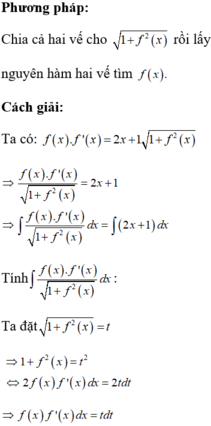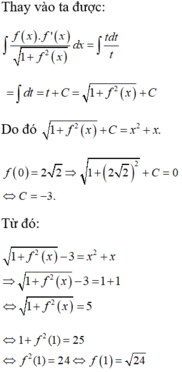Cho hàm số y=f(x)=2x+1 khi đó f (0) có giá trị là

Những câu hỏi liên quan
Cho hàm số y=f(x) có đúng ba điểm cực trị là - 2 ; - 1 ; 0 và có đạo hàm liên tục trên R. Khi đó hàm số y = f ( x 2 - 2 x ) có bao nhiêu điểm cực trị?
A. 6
B. 4
C. 5
D. 3
Cho y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x - 3 ) 2 . Khi đó số cực trị của hàm số y = f ( 2 x + 1 ) là
A. 0
B. 2
C. 1
D. 3
Cho hàm số y=f(x)=2x^2 -8
a) Tính f(–3) ; f(0) ; f(1) ; f(2) b) Tìm giá trị của x để f(x) có giá trị bằng 0.
a: f(-3)=10
f(0)=-8
f(1)=-6
f(2)=0
b: f(x)=0
=>(x-2)(x+2)=0
=>x=2 hoặc x=-2
Đúng 0
Bình luận (0)
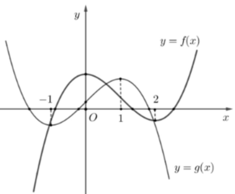
Cho hai hàm số yf(x); yg(x) có đạo hàm trên R và có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số yf(x) Biết rằng hai hàm số yf(-2x+1) và
y
g
a
x
+
b
a
b
∈
ℝ
;
a
#
0
có cùng khoảng đồng biến. G...
Đọc tiếp
Cho hai hàm số y=f(x); y=g(x) có đạo hàm trên R và có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Biết rằng hai hàm số y=f(-2x+1) và y = g a x + b a b ∈ ℝ ; a # 0 có cùng khoảng đồng biến. Giá trị của a + 2b bằng
A. 3
B. 4
C. 2
D. 6
Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 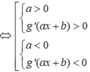
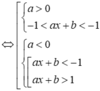
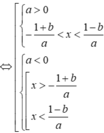
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
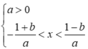 và
và 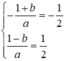
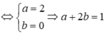
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có f’ (x) liên tục trên nửa khoảng [0;+∞) thỏa mãn biết 3f(x) + f(x)
1
+
3
e
-
2
x
. Giá trị f(0)
11
3
. Giá trị f
1
2
ln...
Đọc tiếp
Cho hàm số y = f(x) có f’ (x) liên tục trên nửa khoảng [0;+∞) thỏa mãn biết 3f(x) + f(x) = 1 + 3 e - 2 x . Giá trị f(0) = 11 3 . Giá trị f 1 2 ln 6 bằng
A. 1 2
B. 5 6 18
C. 1
D. 5 6 9
Đáp án B
Phương pháp: Đạo hàm: ![]()
Cách giải:

![]()
![]()

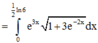
Ta có:
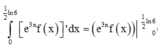

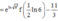
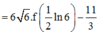


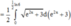
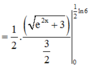
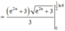
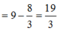
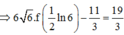
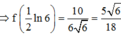
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện:
f
(
0
)
2
3
,
f
(
x
)
0
,
∀
x
∈
ℝ
và
f
(
x
)
.
f
(
x
)
(
2
x
+
1
)
1
+
f...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f ( 0 ) = 2 3 , f ( x ) > 0 , ∀ x ∈ ℝ và f ( x ) . f ' ( x ) = ( 2 x + 1 ) 1 + f 2 ( x ) , ∀ x ∈ ℝ . Khi đó giá trị f(1) bằng:
![]()
![]()
![]()
![]()
cho hàm số y = f(x) = 2x - 1
a, tính f(-2) ; f(0)
b, tính giá trị của x khi y=1
a)
thay f(x) = f(-2) ta được : y = 2 x (-2) - 1 = -5
thay f(x) =f(0) ta được : y = 2 x 0 - 1= -1
b)
thay y = 1 ta được : 1 = 2x - 1
-2x = -1 - 1
-2x = -2
x = 1
Đúng 1
Bình luận (0)
a) Ta có: f(- 2) = 2. (- 2) - 1 = - 5
Vậy: f(-2 ) = - 5
Ta có: f(0) = 2. 0 - 1 = -1
Vậy: f(0) = -1
Câu b tự làm nhé
Đúng 0
Bình luận (0)
a) f(-2) = 2(-2) - 1
=> 2(-2) - 1= -4 - 1 = -5
=> f(x)=-5
f(0) = 2(0) - 1
=> 2(0) - 1= 0 -1= -1
=> f(0)=-1
b) ta có: y=2x - 1=1
=> 2x - 1=1
2x=1+1
2x=2
x=2:2=1
=> x=1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
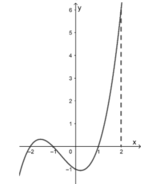
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
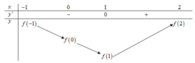
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) (3x2+2x)e-f(x)
∀
x
∈
-
1
;
0
Tính giá trị biểu thức Af(0)-f(-1)
Đọc tiếp
Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x2+2x)e-f(x) ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1)
![]()
![]()
![]()
![]()