
ko giải cách tam giác đồng dạng nha

tui chưa hok tam giác đồng dạng nha giải theo cách định lý thalès vs hệ quả của thalès
vậy thì mình xin giới thiệu luôn hai tam giác đồng dạng luôn: Định nghĩa hai tam giác đồng dạng: Hai tam giác ABC và A'B'C' gọi là đồng dạng với nhau khi chúng có các cặp cạnh tương ứng tỉ lệ và các góc tương ứng bằng nhau
a: Xét ΔEAB và ΔECM có
\(\widehat{EAB}=\widehat{ECM}\)(hai góc so le trong, AB//CM)
\(\widehat{AEB}=\widehat{CEM}\)(hai góc đối đỉnh)
Do đó: ΔEAB đồng dạng với ΔECM(g-g)
=>\(\dfrac{EA}{EC}=\dfrac{AB}{CM}=\dfrac{EB}{EM}\)
\(\dfrac{EA}{EC}=\dfrac{AB}{CM}\)
mà \(CM=\dfrac{CD}{2}\)
nên \(\dfrac{EA}{EC}=AB:\dfrac{CD}{2}=\dfrac{2\cdot AB}{CD}\)
b: Xét ΔFAB và ΔFMD có
\(\widehat{FAB}=\widehat{FMD}\)(hai góc so le trong, AB//DM)
\(\widehat{AFB}=\widehat{MFD}\)(hai góc đối đỉnh)
Do đó: ΔFAB đồng dạng với ΔFMD
=>\(\dfrac{FA}{FM}=\dfrac{FB}{MD}=\dfrac{AB}{MD}\)
Ta có: \(\dfrac{FA}{FM}=\dfrac{AB}{MD}\)
\(\dfrac{BE}{EM}=\dfrac{BA}{MC}\)
mà MD=MC
nên \(\dfrac{FA}{FM}=\dfrac{BE}{BM}\)
=>\(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
Xét ΔMAB có \(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
nên FE//AB
Ta có: FE//AB
AB//CD
Do đó: FE//CD
c: Xét ΔADM có HF//DM
nên \(\dfrac{HF}{DM}=\dfrac{AF}{AM}\)
Xét ΔBDM có FE//DM
nên \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
Xét ΔBMC có EG//MC
nên \(\dfrac{EG}{MC}=\dfrac{BE}{BM}\)
Ta có: \(\dfrac{FE}{DM}=\dfrac{BE}{BM}\)
\(\dfrac{EG}{MC}=\dfrac{BE}{BM}\)
Do đó: \(\dfrac{FE}{DM}=\dfrac{EG}{MC}\)
mà DM=MC
nên FE=EG
Ta có: \(\dfrac{AF}{FM}=\dfrac{BE}{EM}\)
=>\(\dfrac{MF}{FA}=\dfrac{ME}{EB}\)
=>\(\dfrac{MF+FA}{FA}=\dfrac{ME+EB}{EB}\)
=>\(\dfrac{MA}{AF}=\dfrac{MB}{EB}\)
=>\(\dfrac{FA}{AM}=\dfrac{BE}{BM}\)
=>\(\dfrac{HF}{DM}=\dfrac{FE}{DM}\)
=>HF=FE
mà FE=EG
nên HF=FE=EG
Không giải bằng cách 2 tam giác đồng dạng

Không mất tính tổng quát, giả sử K nằm cùng phía so với A trên nửa mp bờ BC
Do BH song song MN, áp dụng định lý Thales trong tam giác ABH:
\(\dfrac{AB}{AM}=\dfrac{AH}{AG}\)
Do CK song song MN, áp dụng định lý Thales trong tam giác ACK:
\(\dfrac{AC}{AN}=\dfrac{AK}{AG}\)
Mặt khác do BH song song CK (cùng song song MN), áp dụng định lý Thales:
\(\dfrac{OH}{OK}=\dfrac{OB}{OC}=1\) (do O là trung điểm BC)
\(\Rightarrow OH=OK\)
Theo tính chất trọng tâm tam giác: \(AG=\dfrac{2}{3}AO\)
Do đó ta có:
\(\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH}{AG}+\dfrac{AK}{AG}=\dfrac{AH+AK}{AG}=\dfrac{\left(OA-OK\right)+\left(OA+OH\right)}{AG}\)
\(=\dfrac{2AO}{AG}=\dfrac{3AG}{AG}=3\)
mọi người cho mình hỏi tam giác này đồng dạng tam giác kia, tam giác kia đồng dạng tam giác nọ, vậy tam giác này có đồng dạng tam giác nọ ko ??
tính chất bắc cầu ý, dc ko ạ ??
Mk nghĩ tam giác này đồng dạng với tam giác nọ
Mk ko chắc lắm đâu , đấy là suy nghĩ của mk thui
tam giác này đồng dạng tam giác kia trường hợp là góc góc
còn tam kia đồng dạng tam giác nọ là trường hợp c-g-c
vậy tam giác này đồng dạng tam giác nọ vẫn đúng à ??
mình đang thắc mắc
hình ở dưới cùng là hình đúng nha
giải thích giúp mik là sao tam giác ADC lại đồng dạng vs tam giác BDH vậy

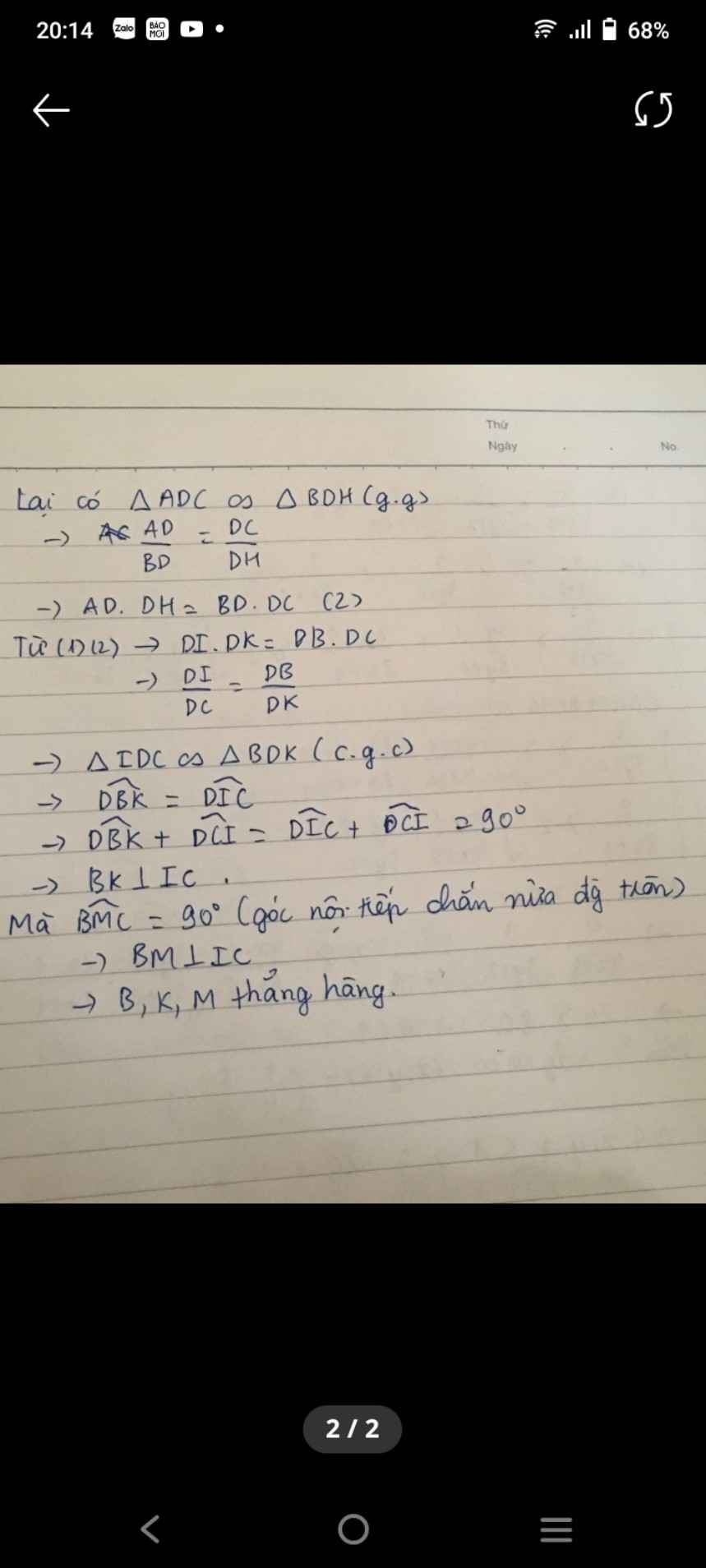
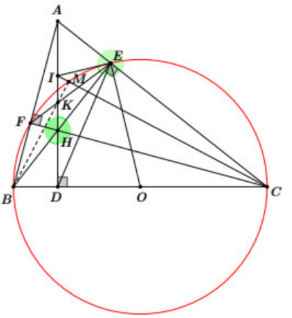
Do \(\widehat{ACD}=\widehat{BHD}\) (cùng phụ \(\widehat{DBH}\)) nên 2 tam giác vuông nói trên đồng dạng
Xét tứ giác BADE có :
\(\left\{{}\begin{matrix}\widehat{BDA}=90^o\left(gt\right)\\\widehat{AEB}=90^o\left(gt\right)\end{matrix}\right.\)
mà 2 góc này nằm ở vị trí kề cùng nhìn 1 cạnh
\(\Rightarrow\) TG BADE nội tiếp (O)
Xét \(\Delta ADC\) và \(\Delta BDH\) có :
\(\widehat{ADC}=\widehat{BDH}\left(=90^o\right)\)
\(\widehat{DAC}=\widehat{EBD}\) (cùng chắn \(\stackrel\frown{DE}\) của đtron \(\left(BADE\right)\) )
\(\Rightarrow\Delta ADC\sim\Delta BDH\left(g-g\right)\)
giải giùm hộ nha bài này tớ băn khoăn lâu rùi nhưng ko giải đc
Tứ giác ABCD có các đường chéo cắt nhau ở O và ko vuông góc với nhau. Gọi H và K lần lượt là trực tâm của các tam giác AOB và COD. Gọi G và I lần lượt là trọng tâm của các tam giác BOC và AOD.
a) Gọi E là trọng tâm của tam giác AOB, F LÀ giao điểm của AH và DK. Chứng minh rằng các tam giác IFG và HFK đồng dạng.
b) Chứng minh rằng IG vuông góc với HK.
Bài 37:Cho tam giác ABC.Hãy vẽ 1 tam giác đồng dạng với tam giác ABC với tỉ số đồng dạng là 3/4(bằng 2 cách).
Cho tam giác ABC đều , Mlà trung điểm BC. Trên cành AB ,AC theo thứ tự lấy các điểm P ,Q sao cho góc PMQ = 60 độ
a) Chứng minh : tam giác MPQ đồng dạng tam giác QCM
b) BP nhân CQ ko đổi
c) CM :tam giác MBP đồng dạng tam giác QMP
d) giả sử góc PMQ =60 độ ko đổi . CMR: khoảng cách từ M đến PQ ko có giá trị thay đổi
e) tính chu vi tam giác APQ theo a (a là cạnh của tam giác ABC)
Bài 37:Cho tam giác ABC.Hãy vẽ 1 tam giác đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\dfrac{3}{4}\)(bằng 2 cách).
Giúp mk giải bài này vs mn!!♥♥
Cho tam giác đều DEF và K là trung điểm của cạnh đáy EF.Một điểm M thay đổi trên cạnh DE sao cho có thể lấy điểm N trên cạnh DF thỏa mãn góc MKN=60 độ. CMR
a) tam giác MEK đồng dạng vs tam giác KFN
b) tam giác MKN đồng dạng với tam giác MEK
c) MK là phân giác của góc EMN
d) Khoảng cách từ điểm K đến đoạn thẳng NM không đổi khi M thay đổi vị trí trên cạnh DE thỏa mãn điều kiện trên.
Cảm ơn mn nha!!