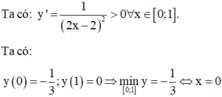tìm x
2x(2x-1)-(2x+5)2=0
\(2x\left(2x-1\right)-\left(2x+5\right)^2=0\)
=>\(4x^2-2x-4x^2-20x-25=0\)
=>-22x-25=0
=>22x+25=0
=>22x=-25
=>\(x=-\dfrac{25}{22}\)
Giải các phương trình sau:
a) x x − 3 + 2 x − 3 = 0 ;
b) x 2 x − 1 − x 2 x + 2 + x 3 − x + 3 = 0
a) Biến đổi về dạng (x - 3)(x + 2) = 0. Tìm được x ∈ { - 2 ; 3 }
b) Thu gọn về dạng -2x + 3 = 0. Tìm được x = 3 2
tìm x
2x.(4x+3)+5=x.(8x+4)+1
2x.(4x+3)+5=x.(8x+4)+1
⇒8x2+6x+5=8x2+4x+1
⇒2x=-4
⇒x=-2
\(2x\left(4x+3\right)+5=x\left(8x+4\right)+1\\ \Leftrightarrow8x^2+6x+5=8x^2+4x+1\\ \Leftrightarrow8x^2-8x^2+6x-4x=1-5\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=-4:2\\ \Leftrightarrow x=-2\)
Vậy \(x=-2\)
Tìm m để bất phương trình x + 2 2 − x 2 x + 2 > m + 4 2 − x + 2 x + 2 có nghiệm?
A. m < − 8
B. m < − 1 − 4 3
C. m < − 7
D. − 8 < m < − 7
Đáp án C
Đặt:
t = 2 − x + 2 x + 2 ⇔ t 2 = x + 4 + 2 2 − x 2 x + 2 ⇔ x + 2 2 − x 2 x + 2 = t 2 − 4
Với x ∈ − 1 ; 2 ta được:
t ' = − 1 2 2 − x + 1 2 x + 2 = 0 ⇔ x = 1 ⇒ 3 ≤ t ≤ 3
Khi đó bất phương trình trở thành:
t 2 − 4 > m + 4 t ⇔ m < f t = t 2 − 4 t − 4 *
Để (*) có nghiệm trên đoạn 3 ; 3 khi và chỉ khi m < max 3 ; 3 f t = − 7
Đồ thị của hai hàm số y = 2 - x 2 x + 1 và y=2x-3 có tất cả bao nhiêu điểm chung ?
A. 3
B. 1
C. 0
D. 2
Giải các phương trình sau:
a) x + 2 x − 2 = 2 x x − 2 + 1 x ;
b) 5 x − 2 3 − x + x + 3 2 − x = 0 ;
c) x 2 x + 2 = 2 x x 2 − 2 x − 3 + x 6 − 2 x ;
d) 4 x 3 − x 2 − x + 1 − 3 1 − x 2 = 1 x + 1 .
Số nghiệm nguyên của bất phương trình x 2 x - 1 ≤ 2 x + 8 x - 1 là
A. 3
B. 4
C. 5
D. 6
Chọn A.
Điều kiện: x > 1
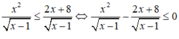
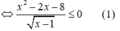
Vì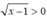 
với ∀x > 1 nên bất phương trình (1) tương đường với x2 - 2x - 8 ≤ 0 ⇔ -2 ≤ x ≤ 4.
Kết hợp với điều kiện x > 1 suy ra 1 ≤ x ≤ 4 ⇒ x ∈ {2;3;4}
Vậy bất phương trình có ba nghiệm nguyên.
Tìm giá trị nhỏ nhất của hàm số y = 1 − x 2 x − 3 trên [0;1]
A. min 0 ; 1 y = − 1 3
B. min 0 ; 1 y = 0
C. min 0 ; 1 y = − 1
D. min 0 ; 1 y = − 2
Phương trình : x 2 x - 3 + x 2 x + 1 = 2 x x + 1 x + 3 có nghiệm là
A. 0
B. 1
C. 2
D. Kết quả khác
