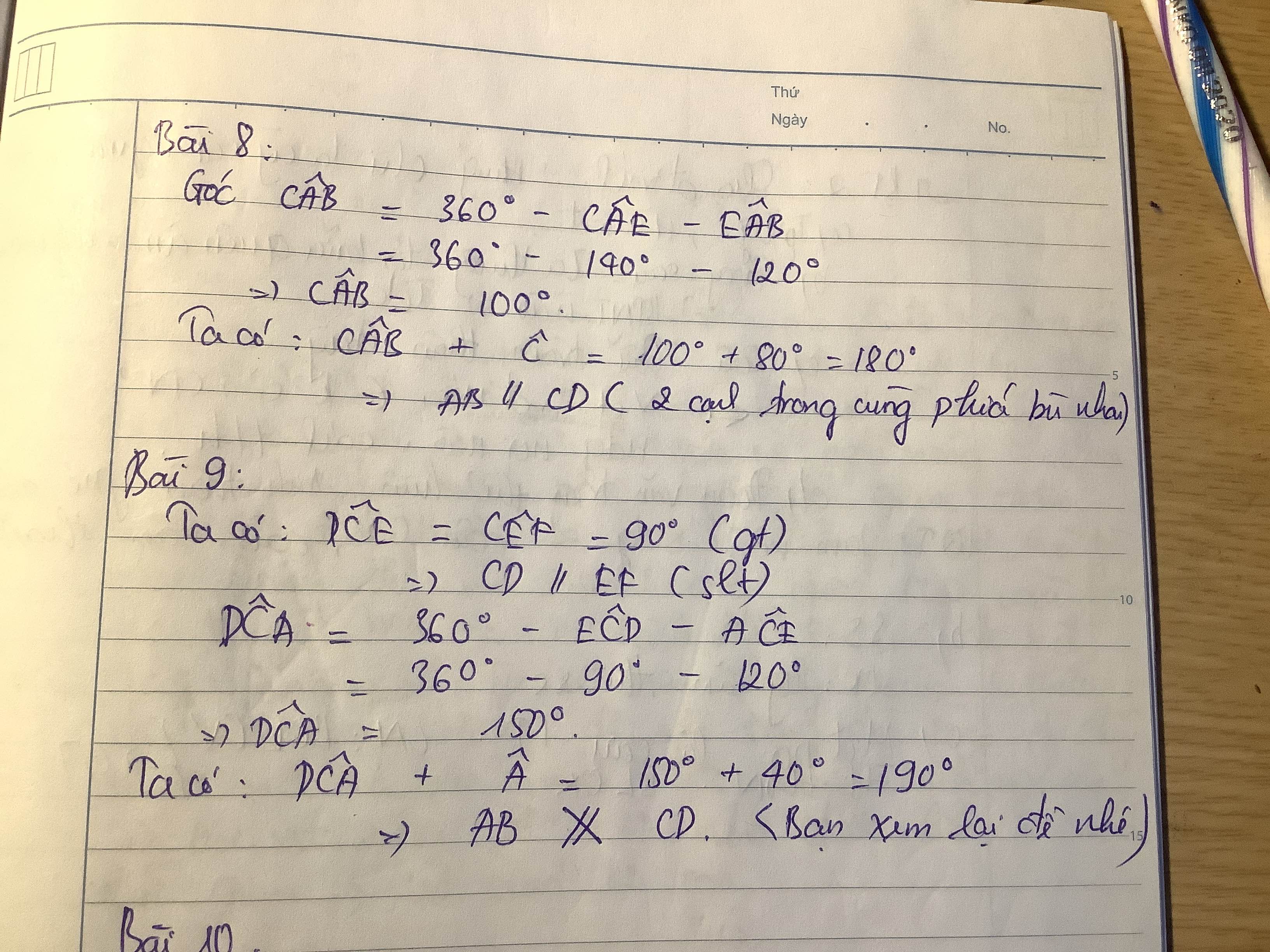gúip mik mấy bài vs
gúip mik mấy bài vs

Những câu hỏi liên quan
Người dân Chư Lênh đón tiếp cô giáo đến như thế nào?
A. Trang trọng
B. Thân mật
C. Trang trọng và thân tình
gúip mik vs
C.Trang trọng và thân tình
Người dân buôn Chư Lênh đón tiếp cô giáo rất Trang trọng và thân tình.
=> Chọn câu: D
Xem thêm câu trả lời
Giúp mik mấy bài này vs mik cần gấp
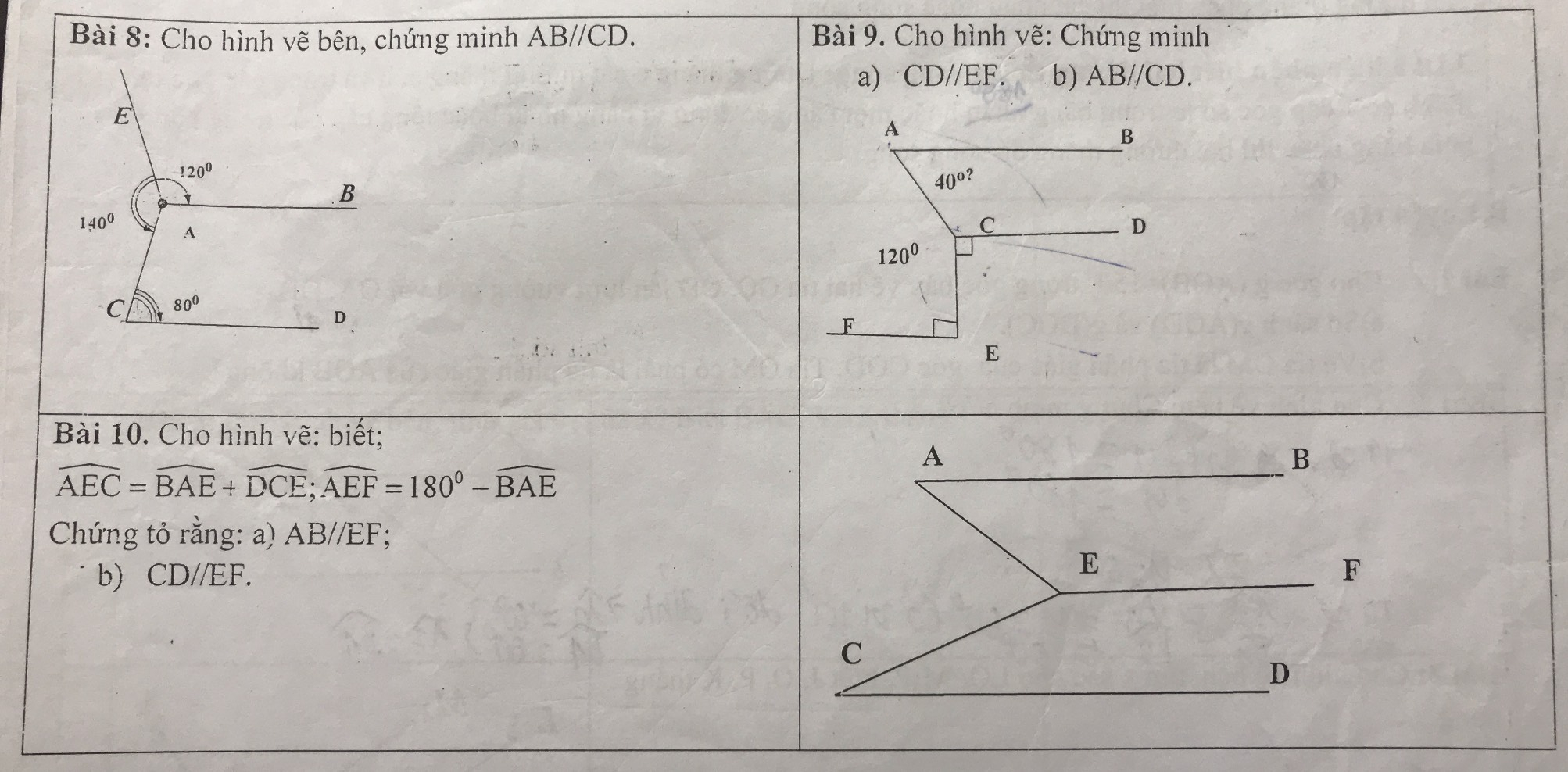
giúp mik mấy bài này vs
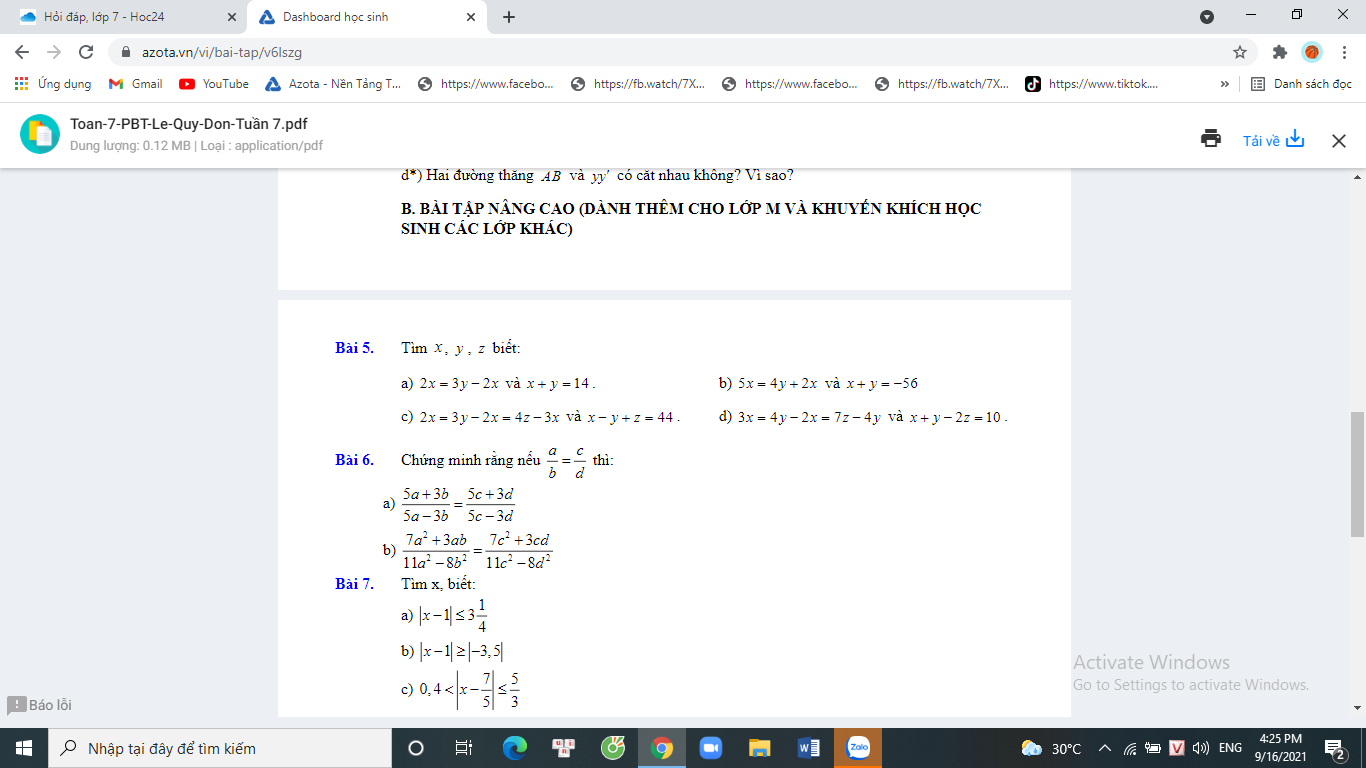
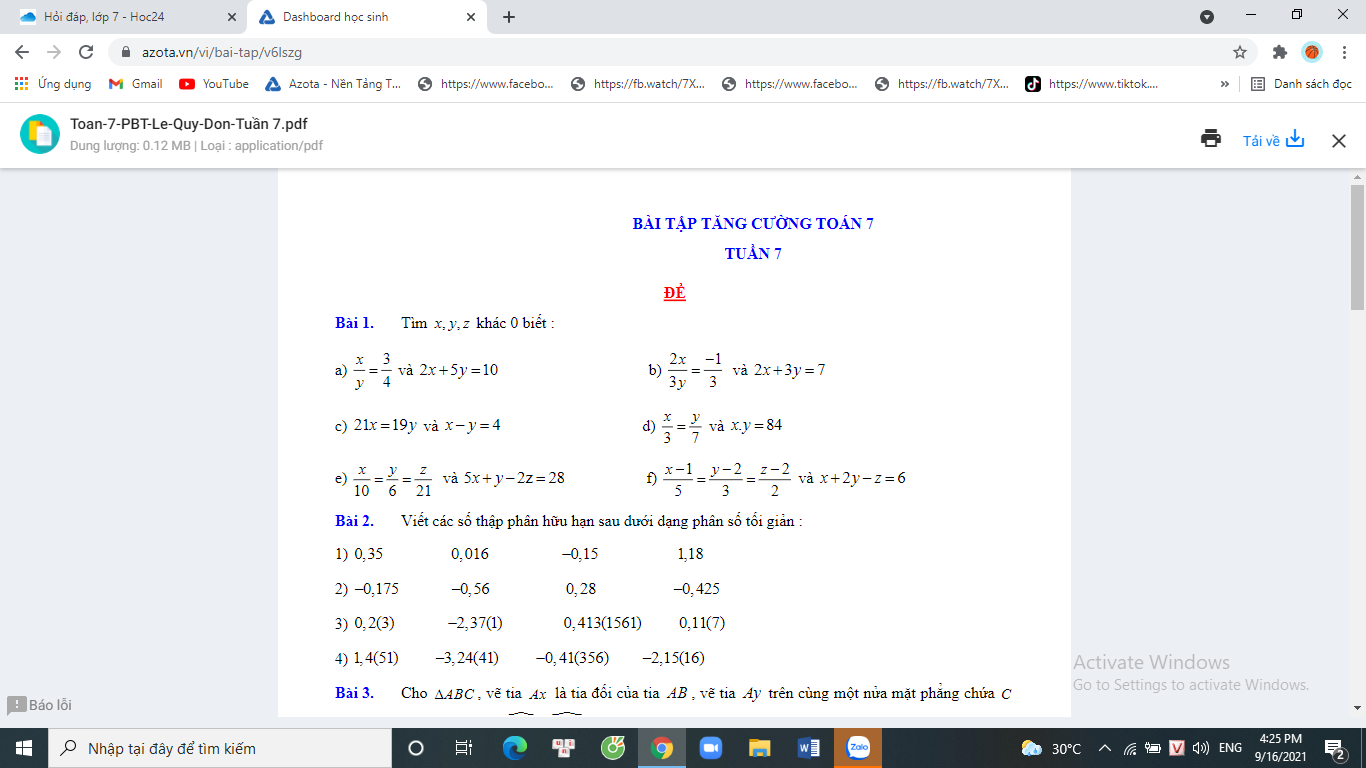
Giúp mik mấy bài này vs.

Mấy bạn giải giúp mik bài 7 và bài 9 vs ạ
Bài 7:
a)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge m+1\\x\ge\dfrac{m}{4}\end{matrix}\right.\)
TH1: \(m+1< \dfrac{m}{4}\Rightarrow m< -\dfrac{4}{3}\)
\(\Rightarrow x\ge\dfrac{m}{4}\)\(\Rightarrow x\in\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
\(\Leftrightarrow\dfrac{m}{4}\ge0\Leftrightarrow m\ge0\) kết hợp với \(m< -\dfrac{4}{3}\Rightarrow m\in\varnothing\)
TH2:\(m+1\ge\dfrac{m}{4}\Rightarrow m\ge-\dfrac{4}{3}\)
\(\Rightarrow x\ge m+1\)\(\Rightarrow\)\(x\in\)\([m+1;+\)\(\infty\))
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([m+1;\)\(+\infty\)\()\)
\(\Leftrightarrow m+1\le0\Leftrightarrow m\le-1\) kết hợp với \(m\ge-\dfrac{4}{3}\)
\(\Rightarrow m\in\left[-\dfrac{4}{3};-1\right]\)
Vậy...
b)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2-m\\x\ne-m\end{matrix}\right.\)\(\Rightarrow x\in\)\([2-m;+\)\(\infty\)) (vì \(-m< 2-m\))
Để hàm số xác ddingj với mọi x dương
\(\Leftrightarrow\left(0;+\infty\right)\subset\)\([2-m;+\)\(\infty\))
\(\Leftrightarrow2-m\le0\Leftrightarrow m\ge2\)
Vậy...
Đúng 2
Bình luận (0)
Bài 9:
a)Đặt \(f\left(x\right)=x^2+2x-2\)
TXĐ:\(D=R\)
TH1:\(x\in\left(-\infty;-1\right)\)
Lấy \(x_1;x_2\in\left(-\infty;-1\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2\)
Vì \(x_1;x_2\in\left(-\infty;-1\right)\Rightarrow x_1+x_2< -1+-1=-2\)\(\Leftrightarrow x_1+x_2+2< 0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;-1\right)\)
TH2:\(x\in\left(-1;+\infty\right)\)
Lấy \(x_1;x_2\in\left(-1;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2>0\)
Suy ra hàm đb trên \(\left(-1;+\infty\right)\)
Vậy...
b)Đặt \(f\left(x\right)=\dfrac{2}{x-3}\)
TXĐ:\(D=R\backslash\left\{3\right\}\)
TH1:\(x\in\left(-\infty;3\right)\)
Lấy \(x_1;x_2\in\left(-\infty;3\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(-\infty;3\right)\Rightarrow x_1-3< 0;x_2-3< 0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;3\right)\)
TH2:\(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(3;+\infty\right)\Rightarrow x_1-3>0;x_2-3>0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(3;+\infty\right)\)
Vậy hàm nb trên \(\left(-\infty;3\right)\) và \(\left(3;+\infty\right)\)
Đúng 2
Bình luận (0)
Mấy bn ơi ,Mấy bn giải giup mik bài này vs càng nhanh càng tốt nha mai mik nộp cho cô r
DTXQ hình lập phương:9,6dm vuông
DTTP:?dm vuông các bn giúp cho mik vs mik cần gấp
đề bài cs sai ko bn ơi sao mink ko tách đc
Giúp mấy bài này vs mik cần gấp .
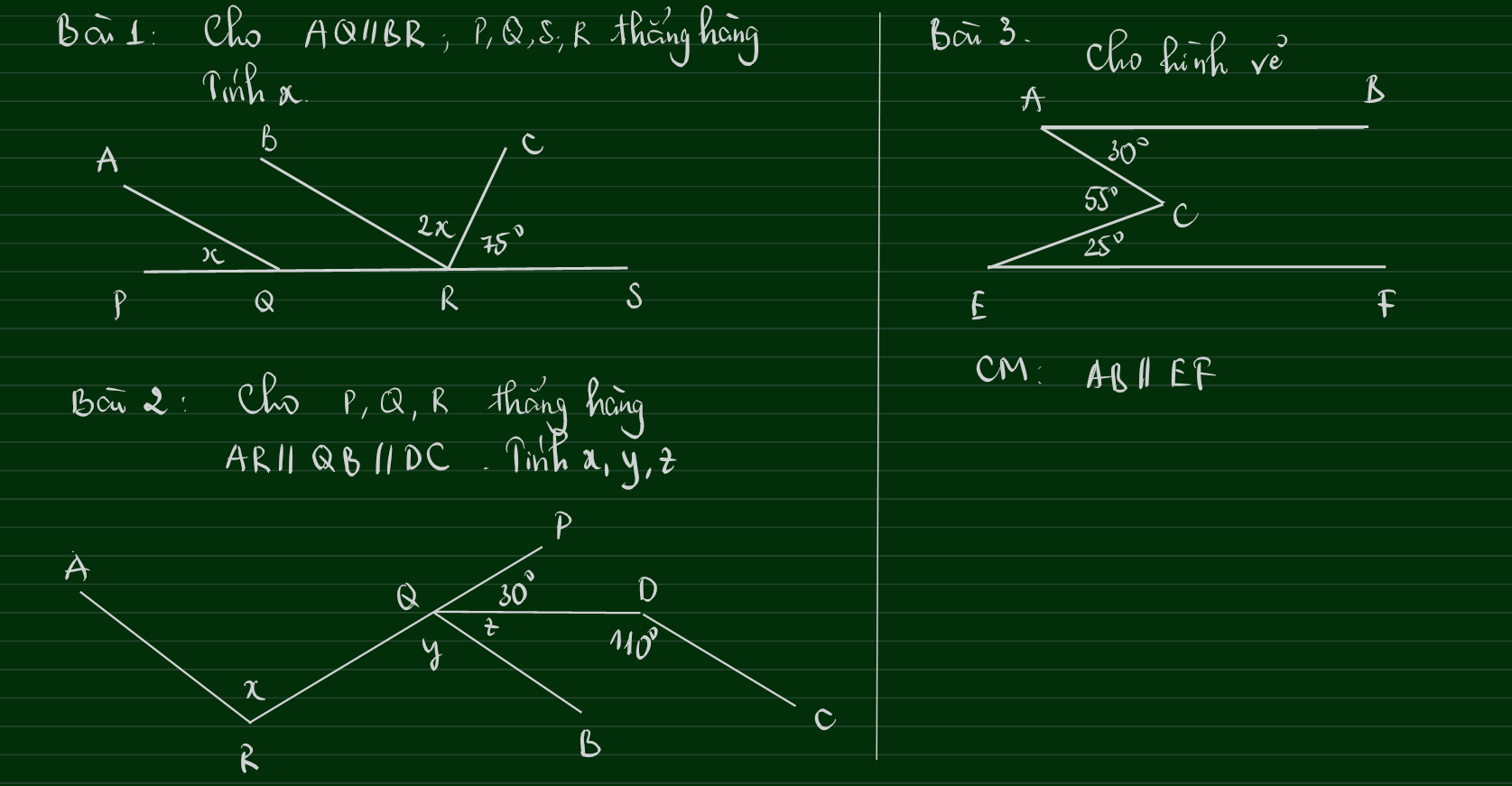
Bài 1:
Vì $AQ\parallel BR$ nên $\widehat{PQA}=\widehat{QRB}$ (hai góc đồng vị )
$\Rightarrow \widehat{QRB}=x$
Lại có:
$Q,R,S$ thẳng hàng nên
$\widehat{QRS}=180^0$
$\widehat{QRB}+\widehat{BRC}+\widehat{CRS}=180^0$
$x+2x+75^0=180^0$
$3x+75^0=180^0$
$x=35^0$
Đúng 1
Bình luận (0)
Bài 2:
Vì $QB\parallel DC$ nên: $\widehat{BQD}+\widehat{QDC}=180^0$ (hai góc trong cùng phía)
$z+110^0=180^0$
$z=70^0$
$P,Q,R$ thẳng hàng
$\Rightarrow \widehat{PQR}=180^0$
$\widehat{RQB}+\widehat{BQD}+\widehat{DQP}=180^0$
$y+z+30^0=180^0$
$y+70^0+30^0=180^0$
$y=80^0$
$AR\parallel QB$
$\Rightarrow x=y=80^0$ (hai góc so le trong)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
bạn nào kb mik vs mik hỏi mấy bài toán