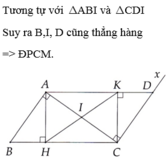
Cho AB // CD, AB = CD sao cho C, B thuộc cùng 1 nửa mặt phẳng bờ AD. Gọi AC giao BD tại O.1. Chứng minh:a) O là trung điểm AC, BDb) AD // BCc) AD = BC2. Kẻ AH ⊥ BD, AH giao CD tại E. CK ⊥ BD, CK giao...

vo huynh thanh toan

27 tháng 2 2016 lúc 19:55

Cho ∆ ABC nhọn. Trên nửa mặt phẳng bờ AB chứa điểm C. Kẻ tia Ax song song với BC. Lấy điểm D thuộc tia Ax sao cho AD = BC. Gọi O là giao của AC, BD a) CMR: O là trung điểm của AC, BD. b) AB//CD c) = d) Gọi I, K lần lượt là trung điểm của AD, CB. CMR: I, O, K thẳng hàng. Bà

Xem chi tiết

Lớp 7 Toán Câu hỏi của OLM

Thanh Bình Nguyễn

3 tháng 12 2023 lúc 14:14

cho Hình thang ABCD có AB // CD O là giao điểm của AC và BD a, chứng mình OA/AC = OB/BD. b, Kẻ đường thẳng đi qua O song song với AD cắt CD tại E. Đường thẳng đi qua O song song với BC cắt CD tại F. Chứng minh DE = CF. c, Gọi I là giao điểm của AD và FO, J là giao điểm của BC và EO. Chứng mình IJ // AB. d, Gọi H là giao điểm của AD và BC K là trung điểm của EF. chứng mminhf O,H,K thẳng hàng

Xem chi tiết

Lớp 8 Toán

Nguyễn Lê Phước Thịnh CTV

3 tháng 12 2023 lúc 14:23

a: Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB\(\sim\)ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)

=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)

=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)

=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)

=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)

b: Xét ΔCAD có OE//AD

nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)

Xét ΔBDC có OF//BC

nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)

=>DE=CF

Đúng 3

Bình luận (0)

Nguyễn Tất Đạt

17 tháng 4 2018 lúc 12:36

Cho tam giác ABC với 3 góc nhọn. Trên nửa mặt phẳng bờ AB chứa điểm C dựng đoạn AE vuông góc với AB sao cho AEAB. Trên nửa mặt phẳng bờ AC chứa điểm B dựng đoạn AD vuông góc với AC sao cho ADAC (Biết rằng D và E cùng thuộc 1 nửa mặt phẳng bờ là BC). Từ A hạ đường cao AH (H thuộc BC), AH giao DE tại N. Gọi M là trung điểm của BC. BE cắt CD tại O. Gọi Bx và Cy lần lượt là tia phân giác của ^DBC và ^ECB và Bx cắt Cy tại điểm I. Lấy K là trung điểm của OI. Hãy chứng minh rằng 3 điểm M;N;K thẳng hàng...

Đọc tiếp

Cho tam giác ABC với 3 góc nhọn. Trên nửa mặt phẳng bờ AB chứa điểm C dựng đoạn AE vuông góc với AB sao cho AE=AB. Trên nửa mặt phẳng bờ AC chứa điểm B dựng đoạn AD vuông góc với AC sao cho AD=AC (Biết rằng D và E cùng thuộc 1 nửa mặt phẳng bờ là BC). Từ A hạ đường cao AH (H thuộc BC), AH giao DE tại N. Gọi M là trung điểm của BC. BE cắt CD tại O. Gọi Bx và Cy lần lượt là tia phân giác của ^DBC và ^ECB và Bx cắt Cy tại điểm I. Lấy K là trung điểm của OI. Hãy chứng minh rằng 3 điểm M;N;K thẳng hàng ?

Xem chi tiết

Lớp 8 Toán Câu hỏi của OLM

Nguyễn Thị Thủy

23 tháng 4 2018 lúc 12:52

Gọi Q là điểm đối xứng với A qua M, S là điểm đối xứng với E qua M

Lấy giao điểm của DB và EC kéo dài là F, gọi G là trung điểm của OF. Nối F với I.

Dễ dàng chứng minh được: \(\Delta\)AMC=\(\Delta\)BMQ (c.g.c) => ^MAC=^MQB

Suy ra AC // BQ (2 góc so le trong bằng nhau) => ^BAC+^ABQ=180⁰ (1)

Ta có: ^BAC+^EAD= 2.^BAC + ^CAE + ^DAB = (^BAC+^CAE) + (^BAC+^DAB) = ^BAE+^CAD=180⁰ (2)

Từ (1) và (2) => ^BAC+^ABQ=^BAC+^EAD => ^ABQ=^EAD

=> \(\Delta\)ABQ=\(\Delta\)EAD (c.g.c) = >^BAQ=^AED (2 góc tương ứng) hay ^BAM=^AEN

Xét \(\Delta\)ABM và \(\Delta\)EAN: ^BAM=^AEN; ^ABM=^EAN (Cùng phụ với ^BAH); AB=AE

=> \(\Delta\)ABM=\(\Delta\)EAN (g.c.g) => AM=EN (2 cạnh tương ứng)

Tương tự ta chứng minh AM=DN => DN=EN => N là trung điểm của DE

\(\Delta\)AEC=\(\Delta\)ABD (c.g.c) => EC=BD

\(\Delta\)EMC=\(\Delta\)SMB (c.g.c) => EC=SB

=> BD=SB => Tam giác DBS cân tại B. Do ^SBF là góc ngoài của \(\Delta\)SDB

=> ^SBF=2. ^BDS .

\(\Delta\)EMC=\(\Delta\)SMB => ^MEC=^MSB => EC//SB hay EF//SB => ^SBF=^EFD (So le trong)

=> ^EFD = 2.^BDS (3)

Dễ thấy Bx và Cy là phân giác 2 góc ngoài của tam giác FBC. Chúng cắt nhau tại I

Nên FI là phân giác của ^CFB hay ^EFD => ^DFI=1/2 ^EFD (4)

Từ (3) và (4) => ^BDS=^DFI => DS//FI (2 góc so le trong)

Mà MN là đường trung bình của tam giác EDS => MN//FI (*)

Xét \(\Delta\)OIF:

K là trung điểm OI, G là trung điểm OF => KG là đường trung bình \(\Delta\)OIF => KG//FI (**)

Xét tứ giác BOCF: M; G lần lượt là trung điểm của 2 đường chéo BC và OF

FB giao CO tại D; FC giao BO tại E; N là trung điểm của DE

Tứ đó ta có: 3 điểm G;M;N cùng nằm trên đường thẳng Gauss của tứ giác BOCF

=> G,M,N thẳng hàng (***)

Từ (*); (**) và (***) => 3 điểm M;N;K thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).

Đúng 0

Bình luận (0)

Trần Lê Việt Hoàng-free...

9 tháng 8 2019 lúc 9:07

ΔAMC=ΔBMQ (c.g.c) => ^MAC=^MQB

Suy ra AC // BQ (2 góc so le trong bằng nhau) => ^BAC+^ABQ=180⁰ (1)

Ta có: ^BAC+^EAD= 2.^BAC + ^CAE + ^DAB = (^BAC+^CAE) + (^BAC+^DAB) = ^BAE+^CAD=180⁰ (2)

Từ (1) và (2) => ^BAC+^ABQ=^BAC+^EAD => ^ABQ=^EAD

=> ΔABQ=ΔEAD (c.g.c) = >^BAQ=^AED (2 góc tương ứng) hay ^BAM=^AEN

Xét ΔABM và ΔEAN: ^BAM=^AEN; ^ABM=^EAN (Cùng phụ với ^BAH); AB=AE

=> ΔABM=ΔEAN (g.c.g) => AM=EN (2 cạnh tương ứng)

Tương tự ta chứng minh AM=DN => DN=EN => N là trung điểm của DE

ΔAEC=ΔABD (c.g.c) => EC=BD

ΔEMC=ΔSMB (c.g.c) => EC=SB

=> BD=SB => Tam giác DBS cân tại B. Do ^SBF là góc ngoài của ΔSDB

=> ^SBF=2. ^BDS .

ΔEMC=ΔSMB => ^MEC=^MSB => EC//SB hay EF//SB => ^SBF=^EFD (So le trong)

=> ^EFD = 2.^BDS (3)

Dễ thấy Bx và Cy là phân giác 2 góc ngoài của tam giác FBC. Chúng cắt nhau tại I

Nên FI là phân giác của ^CFB hay ^EFD => ^DFI=1/2 ^EFD (4)

Từ (3) và (4) => ^BDS=^DFI => DS//FI (2 góc so le trong)

Mà MN là đường trung bình của tam giác EDS => MN//FI (*)

Xét ΔOIF:

K là trung điểm OI, G là trung điểm OF => KG là đường trung bình ΔOIF => KG//FI (**)

Xét tứ giác BOCF: M; G lần lượt là trung điểm của 2 đường chéo BC và OF

FB giao CO tại D; FC giao BO tại E; N là trung điểm của DE

Tứ đó ta có: 3 điểm G;M;N cùng nằm trên đường thẳng Gauss của tứ giác BOCF

=> G,M,N thẳng hàng (***)

Từ (*); (**) và (***) => 3 điểm M;N;K thẳng hàng (Theo tiên đề Ơ-clit) (đpcm).

Đúng 0

Bình luận (0)

nguyen the quan

5 tháng 11 2019 lúc 18:55

a) Ta có: góc FAB + góc BAC = 90 độ
góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC

b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM

c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.a) Ta có: góc FAB + góc BAC = 90 độ

góc EAC + góc BAC = 90 độ
=> Góc FAB = góc EAC
AF=AC; AB=AE
=> Tam giác AFB = tam giác ACE
=> FB=EC

b) Lấy K sao cho M là trung điểm của AK thì ta có ACKB là hình bình hành nên góc ACB =180* - góc BAC. Ta cũng tính dc góc FAE= 180* - góc BAC ( tổng của BAC với 2 lần góc CAE, mà góc CAE=90* -góc BAC). Thêm với AC=AF , CK=AE (=AB) nên tam giác ACK = tam giác FAE nên AK=EF mà AK=2AM nên EF=2AM

c) Gọi H là giao của AM và EF. Tam giác ACK = tam giác FAE nên góc CAK = góc AFE, mà góc CAK phụ với góc MAF nên góc AFE cũng phụ góc MAF. Xét trong tam giác AHF có góc F và góc A phụ nhau nên tam giác AHF vuông tại H suy ra AM vuông góc với EF.