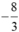F=x^13-9x^12+9x^11-9x^10+.....-9x^2+9x-2 với x=8
Tính giá trị biểu thức trên 1 cách hợp lý
`x^13-9x^12+9x^11-9x^10+....-9x^2+9x-2`
với ` x=2024`
Sửa đề: x=8
Khi x=8 thì x+1=9
\(x^{13}-9x^{12}+9x^{11}-9x^{10}+\cdots-9x^2+9x-2\)
\(=x^{13}-x^{12}\left(x+1\right)+x^{11}\left(x+1\right)-x^{10}\left(x+1\right)+\cdots-x^2\left(x+1\right)+x\left(x+1\right)-2\)
\(=x^{13}-x^{13}-x^{12}+x^{12}+x^{11}-x^{11}-x^{10}+\cdots-x^3-x^2+x^2+x-2\)
=x-2
=8-2
=6
x^13 - 9x^12 + 9x^11 - 9x^10 +...-9x^2 + 9x -2 với x = 8
\(8^{13}-9.8^{12}+9.8^{11}-9.8^{10}+.....-9.8^2+9.8-2\)
\(=8^{13}-\left(8+1\right).8^{12}+\left(8+1\right).8^{11}-\left(8+1\right).8^{10}+....-\left(8+1\right).8^2+\left(8+1\right).8-2\)
\(=8^{13}-8^{13}-8^{12}+8^{12}+8^{11}-8^{11}-8^{10}+....-8^3-8^2+8^2+8-2\)
\(=\left(8^{13}-8^{13}\right)-\left(8^{12}-8^{12}\right)+\left(8^{11}-8^{11}\right)-....-\left(8^2-8^2\right)+8-2\)
\(=8-2=6\)
rút gọn biểu thức B=gá trị tuyệt đối của x+10/x64+9x^3-9x^2+9x-10
Bài 4 chứng minh các biểu thức ko thuộc giá trị của biến
c)( x-3) (x^2+3x+9)-x^3
D) ( 3x+2 )(9x^2 -6x+4) -9x (3x^2+1)+9x
Lời giải:
c.
$(x-3)(x^2+3x+9)-x^3=x^3-3^3-x^3=-27$ không phụ thuộc vào giá trị của biến
Ta có đpcm
d.
$(3x+2)(9x^2-6x+4)-9x(3x^2+1)+9x$
$=(3x)^3+2^3-27x^3-9x+9x$
$=27x^3+8-27x^3=8$ không phụ thuộc vào giá trị của biến
Ta có đpcm
c) Ta có: \(\left(x-3\right)\left(x^2+3x+9\right)-x^3\)
\(=x^3-27-x^3\)
=-27
d) Ta có: \(\left(3x+2\right)\left(9x^2-6x+4\right)-9x\left(3x^2+1\right)+9x\)
\(=27x^3+8-27x^3-9x+9x\)
=8
cho x>0 . tìm giá trị nhỏ nhất của biểu thức S = \(9x^2-5x+\frac{1}{9x}+10\)
Tìm 2 nghiệm của đa thức sau F(x)= x10 - 9x9 + 9x8 - 9x7 +....+ 9x2 - 9x+8
Để F(x) có nghiệm <=> x^10 - 9x^9 + ... + 9x^2 - 9x +8 = 0
<=> (x^10 - x^9) - (8x^9 - 8x^8) + (x^8 - x^7) - ... + (x^2 - x) - (8x - 8) = 0
<=> x^9(x - 1) - 8x^8(x - 1) + ... + x(x - 1) - 8(x - 1) = 0
<=> (x^9 - 8x^8 + ... + x - 8)(x - 1) = 0
<=> ( (x^9 - 8x^8) + (x^7 - 8x^6) + ... + (x - 8) )(x - 1) = 0
<=> (x^8 + x^6 + ... + 1)(x - 8)(x - 1) = 0
Có nghiệm là 8 và 1
Cho x > 0. Tìm giá trị nhỏ nhất của biểu thức
\(A=9x^2-5x+\frac{1}{9x}+10\)
\(A=\left(9x^2-6x+1\right)+\left(x+\frac{1}{9x}\right)+9\)
\(=\left(3x-1\right)^2+\left(x+\frac{1}{9x}\right)+9\)
\(\ge0+2\sqrt{x.\frac{1}{9x}}+9\)
\(=0+\frac{2}{3}+9=\frac{29}{3}\)
chứng minh rằng : Giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến
A= (3x - 1) (9x2 + 3x + 1) + (1- 3x)3 - 3x(9x - 3) - (x+2)3 + x(x2 +6x - 12)
Tính giá trị của biểu thức 3x2 – 9x tại x = 1 và tại x = 1 3 .
- Thay x = 1 vào biểu thức 3x2 – 9x, ta có:
3.12-9.1 = 3.1 - 9 = 3 - 9 = -6
Vậy giá trị của biểu thức 3x2 – 9x tại x = 1 là – 6
- Thay 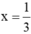 vào biểu thức trên, ta có:
vào biểu thức trên, ta có:
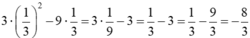
Vậy giá trị của biểu thức 3x2 – 9x tại 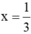 là
là