Tìm hai số a và b biết rằng ƯCLN(a,b) = 6 và BCNN(a,b) = 180
Tìm hai số tự nhiên a,b biết:
a)ƯCLN(a,b)=6 và a.b=216
b,ƯCLN(a,b)=16 và BCNN(a,b)=240
c)BCNN(a,b)=60 và a.b=180
bài này t biết làm nè nhưng dài quá bạn có zalo ko mik chụp cho
Tìm số tự nhiên a và b biết rằng :
a) ƯCLN(a;b) = 15 và BCNN(a;b) gấp ƯCLN(a;b) 2100 lần
b) a . b = 180 và BCNN(a;b) gấp 20 lần ƯCLN(a;b)
Tìm hai số a và b biết rằng ƯCLN(a,b) = 6 và BCNN(a,b) = 120
Vì (a,b) = 6 nên a = 6x, b = 6y, với (x,y)=1
Suy ra a.b=6x.6y = 36xy.
Lại có a.b = [a,b].(a,b) = 120.6 = 720
Suy ra 36xy = 720 => xy = 20
Giả sử x < y, và (x,y)=1 ta có các trường hợp sau:
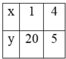
Từ đó suy ra a,b có các trường hợp sau:
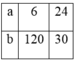
Tìm hai số a và b biết rằng ƯCLN(a,b) = 6 và BCNN(a,b) = 120
Tìm hai số tự nhiên a và b biết a > b, a + b = 16 và ƯCLN ( a ,b ) = 4 b) Tìm 2 số tự nhiên a và b biết BCNN ( a, b ) = 180, ƯCLN ( a, b ) =12
Tìm 2 số nguyên dương a và b biết:
a, BCNN(a;b) = 240 và ƯCLN(a;b)
b, a.b = 180 và BCNN(a;b) = 60
c, a.b = 216 và ƯCLN(a;b) = 6
d, a:b = 2,6 và ƯCLN(a;b) = 5
e, a + b = 42 và BCNN(a;b) = 72
Câu hỏi của Bùi Đức Lộc - Tiếng Việt lớp 1 - Học toán với OnlineMath
Nhớ xem và !
a, 24 và 10
b, 6 và 30
c, 6 và 36
d, <không có trường hợp nào>
e, 36 và 6
Chúc bạn học giỏi !
<Lưu ý : Bạn xem lại câu d>
d) Do (a,b) = 5 => a = 5m
b = 5n
( m,n ) = 1
a : b = 2,6 => a/b = 13/5 = 5m/5n => m = 13 ; n =5
=> a = 65 b = 25
Tìm 2 số nguyên dương a,b biết
a, BCNN(a,b)=240 và ƯCLN(a,b)=16
b, a.b=216 và ƯCLN(a,b)=6
c, a.b=180 và BCNN(a,b)=60
d, a:b=2,6 và ƯCLN(a,b)=5
e, a+b=42 vag BCNN(a,b)=72
tìm hai số tự nhiên a và b biết BCNN(a,b) = 180 và ƯCLN (a,b) = 12
Tìm các số tự nhiên a và b (a<b), biết:
a) ƯCLN ( a, b ) = 15 và BCNN ( a, b ) = 180
b) ƯCLN ( a, b ) = 11 và BCNN ( a, b ) = 484
Trước tiên, ta cần chứng minh 2 bổ đề sau:
Bổ đề 1: Cho 2 số tự nhiên \(a,b\) khác 0. Khi đó \(ƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b\).
Bổ đề 2: Cho 2 số tự nhiên \(a,b\) khác 0. Khi đó:\(ƯCLN\left(a,b\right)+BCNN\left(a,b\right)\ge a+b\)
Chứng minh:
Bổ đề 1: Đặt \(\left(a,b\right)=1\) (từ nay ta sẽ kí hiệu \(\left(a,b\right)=ƯCLN\left(a,b\right)\) và \(\left[a;b\right]=BCNN\left(a,b\right)\) cho gọn) \(\Rightarrow\left\{{}\begin{matrix}a=dk\\b=dl\end{matrix}\right.\left(\left(k,l\right)=1\right)\)
Nên \(\left[a,b\right]=dkl\) \(\Rightarrow\left(a;b\right)\left[a;b\right]=dk.dl=ab\). Ta có đpcm.
Bổ đề 2: Vẫn giữ nguyên kí hiệu như ở chứng minh bổ đề 1. Ta có \(k\ge1,l\ge1\) nên \(\left(k-1\right)\left(l-1\right)\ge0\)
\(\Leftrightarrow kl-k-l+1\ge0\)
\(\Leftrightarrow kl+1\ge k+l\)
\(\Leftrightarrow dkl+d\ge dk+dl\)
\(\Leftrightarrow\left[a,b\right]+\left(a,b\right)\ge a+b\) (đpcm)
Vậy 2 bổ đề đã được chứng minh.
a) Áp dụng bổ đề 1, ta có \(ab=\left(a,b\right)\left[a,b\right]=15.180=2700\) và \(a+b\le\left(a,b\right)+\left[a,b\right]=195\). Do \(b\ge a\) \(\Rightarrow a^2\le2700\Leftrightarrow a\le51\)
Mà \(15|a\) nên ta đi tìm các bội của 15 mà nhỏ hơn 51:
\(a\in\left\{15;30;45\right\}\)
Khi đó nếu \(a=15\) thì \(b=180\) (thỏa)
Nếu \(a=30\) thì \(b=90\) (loại)
Nếu \(a=45\) thì \(b=60\) (thỏa)
Vậy có 2 cặp số a,b thỏa mãn ycbt là \(15,180\) và \(45,60\)
Câu b làm tương tự.