bỏ mặc rồi tính cách hợp lý:
a) (14+38+66)-(10+4-16)
b) (70+20-60)-(-30-80+120)
Tính Nhanh: (1/10) + (4/20) + (9/30) + (16/40) + (25/50) + (36/60) + (49/70) + (6+80) + (81/90) + (100/100) = ?
A.66/35 B.55/1000
C.55/100 D.1234/5678
GIẢI ĐẦY ĐỦ NHANH VÀ ĐÚNG!![]()
bài 1 : tính bằng cách thuận tiện.
1/10 + 4/20 + 9/30 + 16/40 + 25/50 + 36/60 + 49/70 + 64/80 + 81/90
\(\dfrac{1}{10}+\dfrac{4}{20}+\dfrac{9}{30}+\dfrac{16}{40}+\dfrac{25}{50}+\dfrac{36}{60}+\dfrac{49}{70}+\dfrac{64}{80}+\dfrac{81}{90}\)
\(=\dfrac{1}{10}+\dfrac{1}{5}+\dfrac{3}{10}+\dfrac{2}{5}+\dfrac{1}{2}+\dfrac{3}{5}+\dfrac{7}{10}+\dfrac{4}{5}+\dfrac{9}{10}\)
\(=\left(\dfrac{1}{10}+\dfrac{3}{10}+\dfrac{7}{10}+\dfrac{9}{10}\right)+\left(\dfrac{1}{5}+\dfrac{2}{5}+\dfrac{3}{5}+\dfrac{4}{5}\right)+\dfrac{1}{2}\)
\(=2+2+\dfrac{1}{2}\)
\(=4+\dfrac{1}{2}\)
\(=\dfrac{8}{2}+\dfrac{1}{2}=\dfrac{9}{2}\)
Tính nhanh:
a,1/4+2/5+6/8+9/15+8/1
b,1/2+2/4+3/6+4/8+5/10+6/12+7/14+8/16+9/18+10/20
c,1/10+4/20+9/30+16/40+25/50+36/60+49/70+64/80+81/90
a; \(\dfrac{1}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{6}{8}\) + \(\dfrac{9}{15}\) + \(\dfrac{8}{1}\)
= (\(\dfrac{1}{4}\) + \(\dfrac{6}{8}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{9}{15}\)) + \(\dfrac{8}{1}\)
= (\(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\)) + 8
= 1 + 1 + 8
= 2 + 8
= 10
b; \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{6}\) + \(\dfrac{4}{8}\) + \(\dfrac{5}{10}\) + \(\dfrac{6}{12}\) + \(\dfrac{7}{14}\) + \(\dfrac{8}{16}\) + \(\dfrac{10}{20}\)
= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x (\(\dfrac{2}{2}\) + \(\dfrac{3}{3}\) + \(\dfrac{4}{4}\) + \(\dfrac{5}{5}\)+ \(\dfrac{6}{6}+\dfrac{7}{7}+\dfrac{8}{8}\) + \(\dfrac{10}{10}\))
= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x (1 + 1 +1 + 1+ 1+ 1+ 1 +1)
= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) x 1 x 8
= \(\dfrac{1}{2}\) + \(\)\(\dfrac{1}{2}\) x 8
= \(\dfrac{1}{2}\) + 4
= \(\dfrac{9}{2}\)
c; \(\dfrac{1}{10}\) + \(\dfrac{4}{20}\) + \(\dfrac{9}{30}\)+\(\dfrac{16}{40}+\dfrac{25}{50}+\dfrac{36}{60}+\dfrac{49}{70}+\dfrac{64}{80}+\dfrac{81}{90}\)
= \(\dfrac{1}{10}+\dfrac{2}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{5}{10}+\dfrac{6}{10}+\dfrac{7}{10}+\dfrac{8}{10}+\dfrac{9}{10}\)
= \(\dfrac{1+2+3+4+5+6+7+8+9}{10}\)
= \(\dfrac{\left(1+9\right)+\left(2+8\right)+\left(3+7\right)+\left(4+6\right)+5}{10}\)
= \(\dfrac{10+10+10+10+5}{10}\)
= \(\dfrac{\left(10+10+10+10\right)+5}{10}\)
= \(\dfrac{10\times4+5}{10}\)
= \(\dfrac{45}{10}\)
= \(\dfrac{9}{2}\)
Tính nhanh:
a,1/4+2/5+6/8+9/15+8/1
b,1/2+2/4+3/6+4/8+5/10+6/12+7/14+8/16+9/18+10/20
c,1/10+4/20+9/30+16/40+25/50+36/60+49/70+64/80+81/90
a; \(\dfrac{1}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{6}{8}\) + \(\dfrac{9}{15}\) + \(\dfrac{8}{1}\)
= (\(\dfrac{1}{4}\) + \(\dfrac{6}{8}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{9}{15}\)) + 8
= (\(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\)) + 8
= 1 + 1 + 8
= 2 + 8
= 10
b; \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{6}\) + \(\dfrac{4}{8}\) + \(\dfrac{5}{10}\) + \(\dfrac{6}{12}\) + \(\dfrac{7}{14}\) + \(\dfrac{8}{16}\) + \(\dfrac{9}{18}\) + \(\dfrac{10}{20}\)
= \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\)
= \(\dfrac{1}{2}\) x 10
= 5
c; \(\dfrac{1}{10}\) + \(\dfrac{4}{20}\) + \(\dfrac{9}{30}\)+\(\dfrac{16}{40}+\dfrac{25}{50}+\dfrac{36}{60}+\dfrac{49}{70}+\dfrac{64}{80}+\dfrac{81}{90}\)
= \(\dfrac{1}{10}+\dfrac{2}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{5}{10}+\dfrac{6}{10}+\dfrac{7}{10}+\dfrac{8}{10}+\dfrac{9}{10}\)
= \(\dfrac{1+2+3+4+5+6+7+8+9}{10}\)
= \(\dfrac{\left(1+9\right)+\left(2+8\right)+\left(3+7\right)+\left(4+6\right)+5}{10}\)
= \(\dfrac{10+10+10+10+5}{10}\)
= \(\dfrac{\left(10+10+10+10\right)+5}{10}\)
= \(\dfrac{10\times4+5}{10}\)
= \(\dfrac{45}{10}\)
= \(\dfrac{9}{2}\)
Đặt tính rồi tính:
70 + 20 80 - 30 10 + 60
20 + 70 80 - 50 90 - 40
Viết phép tính sao cho các chữ số cùng hàng thẳng cột với nhau.
Tính theo thứ tự từ phải sang trái.
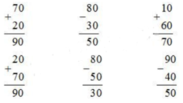
tính bằng cách thuận tiện nhất
1/10 + 4/20+9/30+16/40+ 25/50+36/60+49/70 +64/80+81/90
\(\frac{1}{10}+\frac{4}{20}+\frac{9}{30}+\frac{16}{40}+\frac{25}{50}\) \(+\frac{36}{60}+\frac{49}{70}+\frac{64}{80}+\frac{81}{90}\)
\(=\frac{1}{10}+\frac{1}{5}+\frac{3}{10}+\frac{2}{5}+\frac{1}{2}+\frac{3}{5}+\frac{7}{10}+\frac{4}{5}+\frac{9}{10}\)
\(=\left(\frac{1}{10}+\frac{9}{10}\right)+\left(\frac{1}{5}+\frac{4}{5}\right)+\left(\frac{3}{10}+\frac{7}{10}\right)+\left(\frac{2}{5}+\frac{3}{5}\right)+\frac{1}{2}\)
\(=1+1+1+1+0,5\)
\(=4+0,5\)
\(=4,5\)
viết hợp sau bằng cách chỉ ra tính chất đặc trưng
A = 0;4;8;12;16; 20
b = 10;15;20;25; 30 ;35 ;40
C = 30 ;40 ;50 ;60 ;70 ;80 ; 90
D = 1;6 ;11 ;16 ; 21 ;26
nhanh nhé mọi người
A : Dãy số cách đều 4 đơn vị
B: Dãy số cách đều 5 đơn vị
C: Dãy số cách đều 10 dơn vị
D : dãy số cách đều 5 đơn vị
Tính rồi viết kết quả dưới dạng số thập phân:
a) \(\dfrac{1}{10}\) + \(\dfrac{4}{20}\) + \(\dfrac{9}{30}\) + \(\dfrac{16}{40}\) + \(\dfrac{25}{50}\) + \(\dfrac{36}{60}\) + \(\dfrac{49}{70}\) + \(\dfrac{64}{80}\) + \(\dfrac{81}{90}\)
b) ( \(\dfrac{4}{5}\) x \(\dfrac{3}{8}\) + \(\dfrac{4}{5}\) x \(\dfrac{5}{8}\) - \(\dfrac{4}{5}\) x \(\dfrac{7}{8}\) ) : \(\dfrac{1}{2}\)
\(a,=\dfrac{1}{10}+\dfrac{2}{10}+\dfrac{3}{10}+\dfrac{4}{10}+\dfrac{5}{10}+\dfrac{6}{10}+\dfrac{7}{10}+\dfrac{8}{10}+\dfrac{9}{10}=\dfrac{45}{10}=4,5\\ b,=\dfrac{4}{5}\times\left(\dfrac{3}{8}+\dfrac{5}{8}-\dfrac{7}{8}\right)\times2=\dfrac{8}{5}\times\dfrac{1}{8}=\dfrac{1}{5}=0,2\)
a) Rút gọn các phân số về tối giản, ta được:
\(\dfrac{1}{10}\)+\(\dfrac{2}{10}\)+\(\dfrac{3}{10}\)+\(\dfrac{4}{10}\)+\(\dfrac{5}{10}\)+\(\dfrac{6}{10}\)+\(\dfrac{7}{10}\)+\(\dfrac{8}{10}\)+\(\dfrac{9}{10}\)= kết quả là \(\dfrac{45}{10}\) ra số thập phân = \(4,5\)
b) \(\dfrac{4}{5}\) \(\times\) \(\left(\dfrac{3}{8}+\dfrac{5}{8}-\dfrac{7}{8}\right)\) = \(\dfrac{4}{5}\times\dfrac{1}{8}\) = \(\dfrac{4}{40}=\dfrac{1}{10}\)\(\div\dfrac{1}{2}\)
= \(\dfrac{2}{10}=0,2\)
Viết tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp sau
a) B = {0; 1; 2; 3; 4; 5; 6; 7}
b) C = {10; 20; 30; 40; 50; 60; 70; 80; 90}
a) B={x∈N/ x<8}
b)C={x∈N/x là số tròn chục < 100}