Đề thiếu dữ kiện rồi bạn

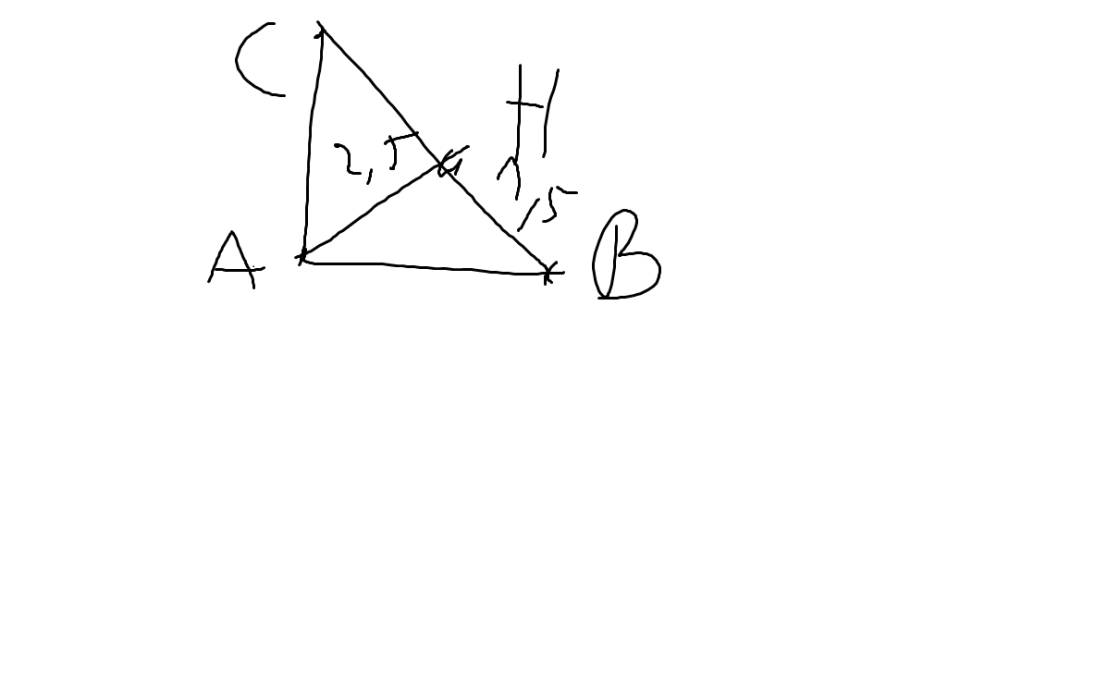
Gọi tam giác vuông đó là ΔABC vuông tại A, AH là đường cao

Theo đề, ta có:

AH=2,5; BH=1,5

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(AB^2=6,25+2,25=8,5\)

=>\(AB=\dfrac{\sqrt{34}}{2}\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AB^2=BH\cdot BC\)

=>\(BC=\dfrac{34}{4}:\dfrac{3}{2}=\dfrac{17}{2}\cdot\dfrac{2}{3}=\dfrac{17}{3}\)

Gọi 2 cạnh tam giác vuông là b và c với \(\dfrac{b}{c}=\dfrac{3}{4}\) \(\Rightarrow b=\dfrac{3}{4}c\)

Cạnh huyền là a với \(a=9,6\left(cm\right)\)

Áp dụng định lý Pitago:

\(b^2+c^2=a^2\Rightarrow\left(\dfrac{3}{4}c\right)^2+c^2=\left(9,6\right)^2\)

\(\Rightarrow c=7,68\left(cm\right)\)

\(b=\dfrac{3}{4}c=5,76\left(cm\right)\)

Áp dụng hệ thức lượng:

\(b^2=ab'\Rightarrow b'=\dfrac{b^2}{a}=3,456\left(cm\right)\)

\(c'=a-b'=6,144\left(cm\right)\)

câu 2

Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125 

Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*) 
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**) 
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0 
=> AB^2 = 5605. Vì AB > 0 => AB = 75 
AC = 4/3 x AC => AC = 100 

Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC. 
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có: 
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45 
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80

(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5

1) Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5

Chọn B.