a) \(a^3-b^3-6ab\)

Những câu hỏi liên quan
\(a^3+b^3\)-6ab+8=0.Tính M=a+b
\(\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-6ab+8=0\)
\(\Leftrightarrow\left(a+b+2\right)\left(a^2+2ab+b^2+4-2a-2b\right)-3ab\left(a+b+2\right)=0\)
\(\Leftrightarrow a+b=-2\)
Đúng 0
Bình luận (0)
giúp mik với, thanks mọi người trước nhìu. Bài 1: rút gọn các biểu thức sau: a) ( a + b ) mũ 3 + ( a - b ) mũ 3 - 6ab mũ 2 b ) ( a + b ) mũ 3 - ( a -b ) mũ 3 - 6ab mũ 2 Bài 2: Cho x + y = 7 , tính giá trị biểu thức a) M = ( x + y ) mũ 3 + 2x mxu 2 + 4xy + 2y mỹ 2 b) N = x mũ 3 + y mũ 3 - 2x mũ 2 - 2y mũ 2 + 3xy( x +y) - 4xy + 3(x + y ) =10
Bài 2:
a: Ta có: \(M=\left(x+y\right)^3+2x^2+4xy+2y^2\)
\(=\left(x+y\right)^3+2\cdot\left(x+y\right)^2\)
\(=7^3+2\cdot7^2=441\)
Đúng 0
Bình luận (0)
Cho a,b là hai số thực sao cho a^3 + b^3 + ( a+b)^3 + 6ab = 16. Tính a+b
Cho a,b > 0 thoả mãn : a^3 + b^3 + 6ab = 8 . CMR : a + b = 2.
Nếu \(a+b=2\) thì :
\(a^3+b^3+6ab=\left(a+b\right)\left(a^2-ab+b^2\right)+6ab=2a^2-2ab+2b^2+6ab\)
\(=2a^2+4ab+2b^2=2\left(a+b\right)^2=2.2^2=8\) (TMĐB)
Vậy \(a^3+b^3+6ab=8\) thì \(a+b=2\)
Đúng 0
Bình luận (0)
Cho các số thực a,b thoả mãn a 3 +b 3 −6ab = −11. Chứng minh rằng − 7 /3 < a+b < −2
`a^3+b^3-6ab=-11<=>(a+b)^3-3ab(a+b)-6ab=-11<=>(a+b)^3-3ab(a+b+2)=-11`
Đặt `{(S=a+b),(P=ab):}`
Khi đó ta có `S^3-3P(S+2)=-11<=>(4(S^3+11))/(3(S+2))=4P`
Lại có `S^2>=4P` nên `S^2>=(4(S^3+11))/(3(S+2))`
`<=>(S^3-6S^2+44)/(3(S+2))<=0(S\ne-2)`
- TH1:
`{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>`$\begin{cases} S\leq-2,30213805\\S> -2\end{cases}$`<=>-2<S<-2,30213805(` Vô lý `)`
- TH2:
`{(S^3-6S^2+44>=0),(3(S+2)<0):}<=>`$\begin{cases} S\geq-2,30213805\\S< -2\end{cases}$`<=>-2,30213805<S<-2`
mà `-7/3=-2,33333...<-2,30213805` nên `-7/3<S<-2(đfcm)`
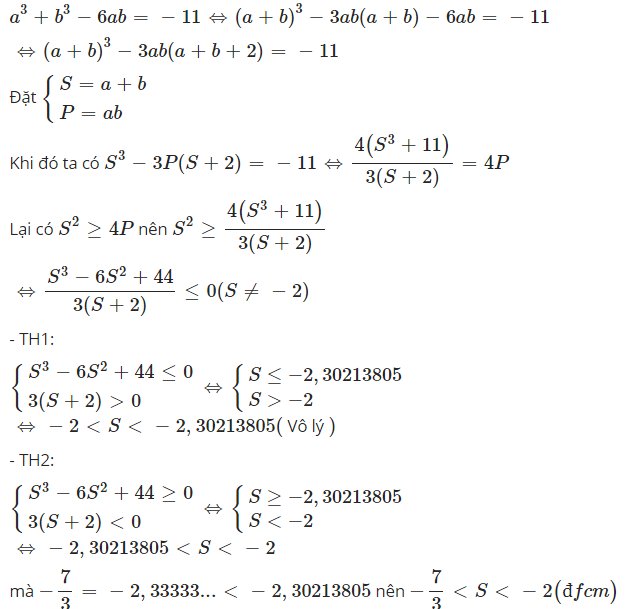
Đúng 1
Bình luận (12)
`a^3+b^3-6ab=-11<=>(a+b)^3-3ab(a+b)-6ab=-11<=>(a+b)^3-3ab(a+b+2)=-11`
Đặt `{(S=a+b),(P=ab):}`
Khi đó ta có `S^3-3P(S+2)=-11<=>(4(S^3+11))/(3(S+2))=4P`
Lại có `S^2>=4P` nên `S^2>=(4(S^3+11))/(3(S+2))`
`<=>(S^3-6S^2+44)/(3(S+2))<=0(S\ne-2)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH1: `{(S^3-6S^2+44<=0),(3(S+2)>0):}<=>{(S<=-2,30213805),(S> -2):}<=>-2<S<-2,30213805(` Vô lý `)`
- TH2: `{(S^3-6S^2+44>=0),(3(S+2)<0):}<=>{(S>=-2,30213805),(S< -2):}<=>-2,30213805<S<-2`
mà `-7/3=-2,33333...<-2,30213805` nên `-7/3<S<-2(đfcm)`
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho a+b=1
Tính M= a^3+b^3+3ab (a^2+b^2)+6ab(a+b)
Ta có
a^3+b^3+3ab(a^2+b^2)+6ab(a+b)=a^3+b^3+3ab.a^2+3ab.b^2+6ab=a^3+b^3+3(a^2)b+3(b^2)a+3a(b-1)b^2+3b(a-1)a^2+6ab
=(a+b)^3+3ab((b-1).b+(a-1).a)+6ab=(a+b)^3+3ab((1-b).(-b)+(1-a)(-a))+6ab=(a+b)^3+3ab(-2ab)+6ab
=(a+b)^3+(-6ab)ab+6ab
=>(a+b)^3+6ab(-ab-1)=6ab(-ab-1)+1 Vậy M=6ab(-ab-1)+1
k cho mình nhá
Đúng 0
Bình luận (0)
Cho a, b là các số thực thỏa mãn \(a^3+b^3\) − 6ab = −11. Chứng minh rằng \(\dfrac{-7}{3}\) < a + b < −2
Rút gọn các biểu thức sau
a)(a+b)^3-(a-b)^3-6a^2-b
b)(a+b)^3+(a-b)^3-6ab^2
\(a,\left(a+b\right)^3-\left(a-b\right)^3-6a^2b\)
\(=a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3-6a^2b\)
\(=2b^3\)
\(b,\left(a+b\right)^3+\left(a-b\right)^3-6ab^2\)
\(=a^3+3a^2b+3ab^2+b^3+a^3-3a^2b+3ab^2-b^3-6ab^2\)
\(=2a^3\)
Đúng 0
Bình luận (0)
cho a,b>0 và \(a^3+b^3+6ab\le8\). tìm GTNN của \(P=\dfrac{1}{a^2+b^2}+\dfrac{3}{ab}+ab\)

















