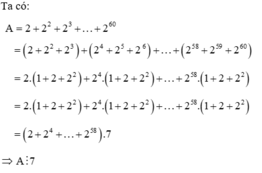Cho A=2+22+23+...+260. Chứng tỏ A chia hết cho 7

Những câu hỏi liên quan
Câu 6: Chứng tỏ A = 2 + 22 + 23 + 24….+ 259 + 260
a. Chia hết cho 3;
b. Chia hết cho 7.
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
A= (2+22+23)+...+(258+259+260)
A=2.(1+2+22)+...+258.(1+2+22)
A=2.7+...+258.7
A=7.(2+...+258)
Vì 7 chia hết cho 7 =>7.(2+...+258) chia hết cho 7
CHIA HẾT CHO 3 :
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
Cho A= 2+22+23+.........+260. Chứng tỏ rằng: A chia hết cho 3;5;7.
Cho A = 2+ 22 + 23 +……+ 260 . Chứng tỏ rằng: A chia hết cho 3, A chia hết cho 7, A chia hết cho 5
Chứng minh rằng A = 2 + 2 2 + 2 3 + … + 2 60 chia hết cho 7.
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |
Đúng 0
Bình luận (0)
Chứng minh rằng A = 2 + 2 2 + 2 3 + . . . + 2 60 chia hết cho 7
Cho H = 2+22+23+.........+260
Hãy chứng tỏ H chia hêt cho 3, 7 và 15
Ta có:
\(H=2+2^2+2^3+...+2^{60}\)
\(H=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(H=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\cdot\left(1+2\right)\)
\(H=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy H chia hết cho 3
_______
\(H=2+2^2+2^3+...+2^{60}\)
\(H=\left(2+2^2+2^3\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(H=2\cdot\left(1+2+4\right)+2^4\cdot\left(1+2+4\right)+...+2^{58}\cdot\left(1+2+4\right)\)
\(H=7\cdot\left(2+2^4+...+2^{58}\right)\)
Vậy H chia hết cho 7
__________
\(H=2+2^2+2^3+...+2^{60}\)
\(H=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(H=2\cdot\left(1+2+4+8\right)+2^5\cdot\left(1+2+4+8\right)+...+2^{57}\cdot\left(1+2+4+8\right)\)
\(H=15\cdot\left(2+2^5+...+2^{57}\right)\)
Vậy H chia hết cho 15
Đúng 3
Bình luận (0)
Ta có:
Ta có:
Ta có:
Vậy H chia hết cho .
nhớ tik đúng nha!!!
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
bài 1:tìm cặp số tự nhiên x,y biết:
1) (x+5)(y-3) = 15
2) xy+2x +3y = 0
3) xy - 2x + y = 9
bài 2:cho A = 2 + 22 + 23 + ...... + 260. chứng tỏ rằng: A chia hết cho 3, 5, 7
mik cần gấp ;-;
h mik ko gấp nữa, nhưng nếu cậu biết cách giải thì chỉ mik nha ạ, làm tư liệu sau này mik học ý ạ :>
Đúng 0
Bình luận (0)
Câu 5: Chứng minh tổng sau chia hết cho 7.
A = 21 + 22 + 23 + 24 +...+ 259 + 260
Đề sai, viết lại thành:
A= 21+22+23+24+...+259+260
Giải:
A=21+22+23+...............+259+260
A=(21+22+23)+...............+(258+259+260)
A=2.(1+2+22)+............+258.(1+2+22)
A=2.7+.......................+258.7
A=(2+24+..............+258).7 ⋮ 7(đpcm)
Đúng 1
Bình luận (1)
Chứng minh rằng C = 2 + 2 2 + 2 3 + . . . + 2 60 chia hết cho 7