a=1

b=9

c=8

tk cho mk,mk đang bị trừ điểm

abc=198 

a = 1 ; b = 9 : c = 8. 

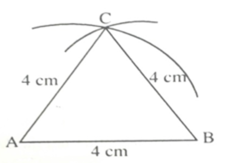
- Vẽ đoạn thẳng AB = 4 cm

- Vẽ cung tròn tâm A bán kính 4 cm

- Vẽ cung tròn tâm B bán kính 4 cm, cắt cung tròn tâm A bán kính 4 cm tại C.

- Vẽ các đoạn thẳng AC, BC. Ta được tam giác ABC.

Đo góc có BAC = ABC = ACB =  60 °

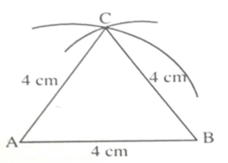
- Vẽ đoạn thẳng AB = 4 cm

- Vẽ cung tròn tâm A bán kính 4 cm

- Vẽ cung tròn tâm B bán kính 4 cm, cắt cung tròn tâm A bán kính 4 cm tại C.

- Vẽ các đoạn thẳng AC, BC. Ta được tam giác ABC.

Đo góc có BAC = ABC = ACB = 60 0

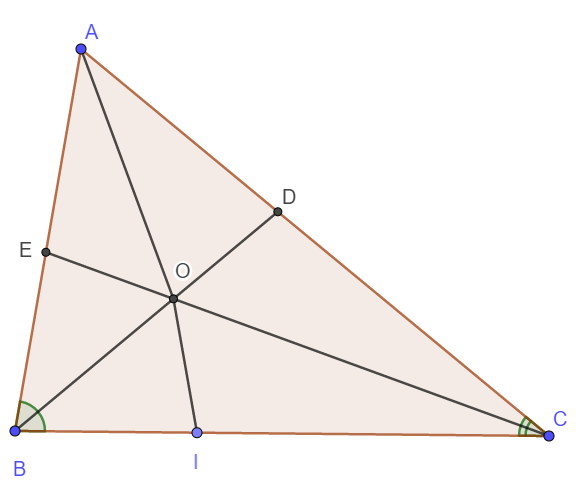
Trên BC lấy điểm I sao cho BI = BE.

Do BC = BE + DC nên IC = DC.

Ta có : \(\Delta EOB=\Delta IOB\left(c-g-c\right)\Rightarrow\widehat{EOB}=\widehat{IOB}\)

\(\Delta DOC=\Delta IOC\left(c-g-c\right)\Rightarrow\widehat{DOC}=\widehat{IOC}\)

Mà \(\widehat{EOB}=\widehat{DOC}\Rightarrow\widehat{EOB}=\widehat{IOB}=\widehat{DOC}=\widehat{IOC}\)

Vậy thì \(\widehat{IOB}=\widehat{DOC}=\widehat{IOC}=\frac{180^o}{3}=60^o\)

\(\Rightarrow\widehat{BOC}=60^o+60^o=120^o\)

\(\Rightarrow\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2}=180^o-120^o=60^o\)

\(\Rightarrow\widehat{B}+\widehat{C}=120^o\Rightarrow\widehat{A}=60^o\)

a, Xét tam giác ECD và tam giác ACB ta có 

^CED = ^CAB = 90⁰

^C _ chung 

Vậy tam giác ECD ~ tam giác ACB ( g.g )

b, Áp dụng định lí Pytago ta có : 

\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=100-36=64\Rightarrow AC=8\)cm 

Do BD là đường phân giác ^B 

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{AD}{DC}\) mà \(DC=AC-AD=8-AD\)

\(\Rightarrow\dfrac{6}{10}=\dfrac{AD}{8-AD}\Rightarrow48-6AD=10AD\Rightarrow16AD=48\Rightarrow AD=3\)cm 

Vậy AD = 3 cm 

c, Ta có : \(\dfrac{S_{ECD}}{S_{ACB}}=\dfrac{\dfrac{1}{2}ED.EC}{\dfrac{1}{2}AC.AB}=\dfrac{ED.EC}{6.8}=\dfrac{ED.EC}{48}\)(*)

\(\dfrac{EC}{AC}=\dfrac{ED}{AB}=\dfrac{CD}{BC}\)( tỉ số đồng dạng ý a ) 

\(\Rightarrow\dfrac{EC}{8}=\dfrac{5}{10}\)( CD = AC - AD = 8 - 3 = 5 cm )

\(\Rightarrow EC=\dfrac{40}{10}=4\) cm (1) 

\(\Rightarrow\dfrac{ED}{AB}=\dfrac{CD}{BC}\Rightarrow ED=\dfrac{AB.CD}{BC}=\dfrac{6.5}{10}=3\)cm (2) 

Thay (1) ; (2) vào (*) ta được :

\(\dfrac{S_{ECD}}{S_{ACB}}=\dfrac{3.4}{48}=\dfrac{12}{48}=\dfrac{1}{4}\)

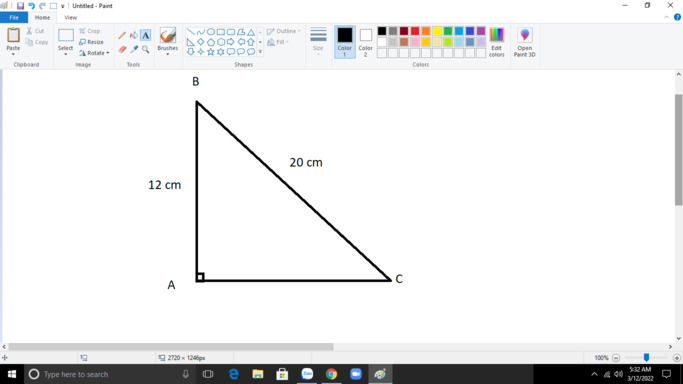
\(\text{Xét }\Delta ABC\text{ có:}\)

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AC^2=BC^2-AB^2\text{(định lí Py ta go đảo)}\)

\(\Rightarrow AC^2=20^2-12^2=400-144=256\left(cm\right)\)

\(\Rightarrow AC=\sqrt{256cm}=16\left(cm\right)\)

\(\text{Xét }\Delta ABC\text{ có:}\)

\(BC>AC>AB\left(20cm>16cm>12cm\right)\)

\(\Rightarrow\widehat{A}>\widehat{B}>\widehat{C}\text{(quan hệ giữa cạnh và góc đối diện trong tam giác)}\)

Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại đây nhé.

Khó vẽ lắm