Cho tam giác ABC vuông tại A,AB=21cm,góc C=40 độ .Tính
a,AC,BC b,Phân giác BD
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 độ. Hãy tính các độ dài
a) AC
b) BC
c) Phân giác BD
Tam giác ABC vuông tại A có AB=21cm, góc \(C=40^0\). Hãy tính các độ dài
a) AC
b) BC
c) Phân giác BD
.cho tam giác vuông ABC ( góc A= 90 độ) AB=28cm, AC=21cm đường phân giác góc A cắt BC tại D đường thẳng qua D và song song với AC, cắt AB tại E.
a) tính BD, BC và DE
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: Phân giác BD
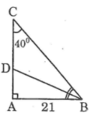
cho tam giác ABC vuông tại A có AB=21cm,C=40 độ.Hãy tính độ dài :AC,BC,phân giác AD
Xét ΔABC vuông tại A có
tan C=AB/AC
=>21/AC=tan 40
=>\(AC\simeq25,03\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}\simeq32,67\left(cm\right)\)
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính độ dài các đoạn thẳng BD,DC và DE.
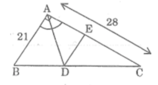
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 21 2 + 28 2 = 1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠ (BAC) nên:
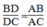 (t/chất đường phân giác)
(t/chất đường phân giác)
Suy ra: 
Hay 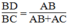
Suy ra: 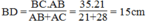
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: 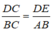 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
Suy ra: 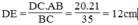
Cho tam giác ABC vuông tại A(góc A=90°),AB=21cm,AC=28cm. Vẽ đường cao AH(H thuộc BC). Tia phân giác của góc A cắt BC tại D. Tính BC,BD,CD và diện tích tam giác AHD
Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(=21^2+28^2\)
\(=1225\)
->\(BC=\sqrt{1225}=35\left(cm\right)\)
Xét ΔABC có AD là tia phân giác ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)
⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)
⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)
Cho tam giác ABC vuông tại A có AB=21cm , AC=28cm.Đường phân giác của góc A cắt BC tại D.Đường thẳng qua DE // AB(E thuộc AC)
a,Tính BD,DC,DE
b, Tính diện tích tam giác ABD và diện tích tam giác ACD.