Cho tam giác ABC cân tại A, đường cao AH. Gọi M là trung điểm của AH, K là chân đường vuông góc kẻ từ H đến CM. CMR góc AKB vuông

Những câu hỏi liên quan
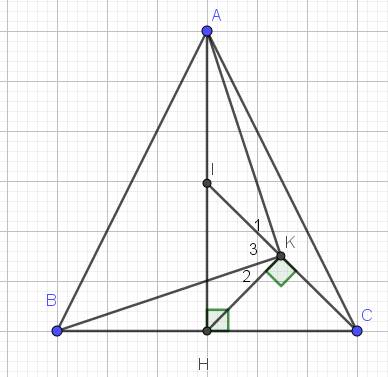
cho tam giác abc cân tại a, đường cao ah. i là trung điểm ah. gọi k là chân đường vuông góc kẻ từ h đến ic. tính akb
Lời giải:
Vì $ABC$ cân tại $A$ nên đường cao $AH$ đồng thời là đường trung tuyến. Hay $H$ là trung điểm $BC$.
Xét tam giác $IHK$ và $HCK$ có:
$\widehat{IHK}=\widehat{HCK}$ (cùng phụ $\widehat{KHC}$)
$\widehat{IKH}=\widehat{HKC}=90^0$
$\Rightarrow \triangle IHK\sim \triangle HCK$ (g.g)
$\Rightarrow \frac{IH}{HK}=\frac{HC}{CK}$
$\Rightarrow \frac{2IH}{HK}=\frac{2HC}{CK}$
$\Rightarrow \frac{AH}{HK}=\frac{BC}{CK}$
Xét tam giác $BKC$ và $AKH$ có:
$\widehat{BCK}=\widehat{AHK}$ (cùng phụ với góc $\widehat{KHC}$)
$\frac{BC}{KC}=\frac{AH}{HK}$ (cmt)
$\Rightarrow \triangle BKC\sim \triangle AKH$ (c.g.c)
$\Rightarrow \widehat{BKC}=\widehat{AKH}$
$\Rightarrow \widehat{K_2}+90^0=\widehat{K_1}+90^0$
$\Rightarrow \widehat{K_2}=\widehat{K_1}$
$\Rightarrow \widehat{K_2}+\widehat{K_3}=\widehat{K_1}+\widehat{K_3}$
$\Rightarrow \widehat{IKH}=\widehat{AKB}$
Hay $90^0=\widehat{AKB}$
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH 12cm; BC 18cmBài 2: Cho tam giác ABC (AC AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:a, DE là đường trung trực của AHb, DEKH là hình thang cânBài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AHb, CM: AI vuôn...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD
mn giúp e
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.
a) CM: AH= DE
b) Gọi I là trung diểm HB, K là trung điểm HC. CMR: DI//EK
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
hay AH=DE
Đúng 1
Bình luận (1)
Cho tam gác abc cân tại a , đường cao ah. Gọi d là chân đường vuông góc kẻ từ h đến ac. I là trung điểm hd
Gọi m là trung điểm cd. Cm mi vuông góc ad
Cm ai vuông góc bd
Cho tam giác cân ABC cân tại A đường cao AH . D là chân đường vuông góc kẻ từ H đến AC . I là trung điểm của HD
a. Gọi M là trung điểm của CD chứng minh MI vuông góc với AH
b. Chứng minh AI vuông góc với BD
Ta có : DM = MC
DI = IH
=> MI là đường trung bình của tam giác vuông MCH
=> MI // HC
Do HC vuông vs AH => MI vuông vs AH ( đpcm )
Đúng 0
Bình luận (0)
mn giúp e
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.
a) CM: AH= DE
b) Gọi I là trung diểm HB, K là trung điểm HC. CMR: DI//EK
mn vẽ cả hình ra giúp e, e cảm ơn
\(a,\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\\ \Rightarrow AEHD\text{ là hcn}\\ \Rightarrow AH=DE\\ b,DI\text{ là tt ứng cạnh huyền }BH\Rightarrow DI=IH\Rightarrow\widehat{IDH}=\widehat{IHD}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{EDH}=\widehat{AHD}\\ \Rightarrow\widehat{IDE}=\widehat{IDH}+\widehat{EDH}=\widehat{IHD}+\widehat{AHD}=\widehat{IHA}=90^0\\ \Rightarrow DI\perp DE\left(1\right)\\ EK\text{ là tt ứng cạnh huyền }CH\Rightarrow EK=KH\Rightarrow\widehat{KEH}=\widehat{KHE}\\ \text{Mà }AEHD\text{ là hcn }\Rightarrow\widehat{AHE}=\widehat{DEH}\\ \Rightarrow\widehat{DEK}=\widehat{DEH}+\widehat{HEK}=\widehat{AHE}+\widehat{KHE}=\widehat{AHK}=90^0\\ \Rightarrow EK\perp DE\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI\text{//}EK\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E theo thứ tự là chân các đường vuông góc kẻ từ H đến a) cm:AH=DE b) Gọi I là trung điểm của HB, K là trung điểm của HC. cm DI//EK
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc kẻ từ H đến AB, AC
a) cm: EF = AH
b) kẻ trung tuyến của tam giác ABC. Cm: AM vuông góc với EF
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H. Gọi K là trung điểm AC, kẻ Ax vuông góc AH cắt HK tại D.
a) CM tứ giác AKHB to hình thang
b) CM tứ giác ADHB là hình bình hành
c) kẻ HN là đường cao tam giác AHB. Gọi I là trung điểm AN, lấy M đối xứng H qua B. CM: MN vuông góc với IH
a: ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có
H,K lần lượt là trung điểm của CB,CA
=>HK là đường trung bình của ΔCAB
=>HK//AB và \(HK=\dfrac{AB}{2}\)
Xét tứ giác AKHB có KH//AB
nên AKHB là hình thang
b: Ta có: AD\(\perp\)AH
BC\(\perp\)AH
Do đó: AD/BC
=>AD//BH
Xét tứ giác ADHB có
AD//HB
AB//HD
Do đó: ADHB là hình bình hành
Đúng 1
Bình luận (0)