Gợi ý : Tìm đ/k của x trong căn thức 

Xét 2 TH : x + 1 > 0 \(;x+1\le0\)

Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:

VT = 5.3 – 2.5 = 15 – 10 = 5 = VP

Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).

Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)

Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:

VT = -3.(-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22 = VP

Vậy (x; y) = (-3; 31/5 ) không phải là nghiệm của phương trình (2).

Hệ phương trình đã cho vô nghiệm.

b) x 4 - 5 x 2  + 4 = 0

Đặt t = x 2  ≥ 0 , ta có phương trình:

t 2  - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)

t 1 = 1 (nhận) ; t 2 = 4 (nhận)

với t = 1 ⇔ x 2  = 1 ⇔ x = ± 1

với t = 4 ⇔  x 2  = 4 ⇔ x = ± 2

Vậy nghiệm của phương trình x = ±1; x = ± 2

a) 3 x 2  – 7x + 2 = 0

Δ= 7 2  -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5

Phương trình có 2 nghiệm phân biệt:

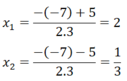
Vậy tập nghiệm của phương trình là S = {2; 1/3}

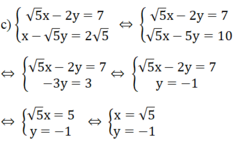
Vậy hệ phương trình có nghiệm (x; y) = ( 5 ; -1)

3:

a: u+v=14 và uv=40

=>u,v là nghiệm của pt là x^2-14x+40=0

=>x=4 hoặc x=10

=>(u,v)=(4;10) hoặc (u,v)=(10;4)

b: u+v=-7 và uv=12

=>u,v là các nghiệm của pt:

x^2+7x+12=0

=>x=-3 hoặc x=-4

=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)

c; u+v=-5 và uv=-24

=>u,v  là các nghiệm của phương trình:

x^2+5x-24=0

=>x=-8 hoặc x=3

=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)

\(x^2-\left(2-\sqrt{3}\right)x-2\sqrt{3}=0\)

\(\Delta=\left[-\left(2-\sqrt{3}\right)^2\right]-4\left(-2\sqrt{3}\right)\) 

\(=\left(4-4\sqrt{3}+3\right)+8\sqrt{3}=7+4\sqrt{3}=\sqrt{3}^2+2.2.\sqrt{3}+2^2=\left(\sqrt{3}+2\right)^2>0\)

=> pt có 2 nghiệm phân biệt

\(\left\{{}\begin{matrix}x_1=\dfrac{2-\sqrt{3}-\sqrt{3}-2}{2}=\dfrac{-2\sqrt{3}}{2}=-\sqrt{3}\\x_2=\dfrac{2-\sqrt{3}+\sqrt{3}+2}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)

Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.

ĐK: $m\neq 0$

a) Khi $m=2,$ hệ phương trình là:

\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)

b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)

c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:

\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)

d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)

Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$