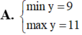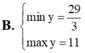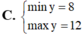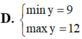Ta có  \(A=\frac{3x^2+9x+17}{3x^2+9x+7}=\frac{\left(3x^2+9x+7\right)+10}{3x^2+9x+7}=\)

\(=\frac{3x^2+9x+7}{3x^2+9x+7}+\frac{10}{3x^2+9x+7}\)

\(=1+\frac{10}{3x^2+9x+7}=1+\frac{10}{3\left(x+\frac{3}{2}\right)^2+\frac{1}{4}}\)

Từ đây suy ra A có GTLN là 41, khi \(x=-\frac{3}{2}\)

1) \(A=\frac{2018x^2-2.2018x+2018^2}{2018x^2}=\frac{\left(x-2018\right)^2+2017x^2}{2018x^2}=\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\)

vì \(\frac{\left(x-2018\right)^2}{2018x^2}\ge0\Rightarrow\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\ge\frac{2017}{2018}\)

dấu = xảy ra khi x-2018=0

=> x=2018

Vậy Min A=\(\frac{2017}{2017}\)khi x=2018

2) \(B=\frac{3x^2+9x+17}{3x^2+9x+7}=\frac{3x^2+9x+7+10}{3x^2+9x+7}=1+\frac{10}{3x^2+9x+7}=1+\frac{10}{3.x^2+9x+7}\)

\(=1+\frac{10}{3.\left(x^2+9x\right)+7}=1+\frac{10}{3.\left[x^2+\frac{2.x.3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{4}+7}=1+\frac{10}{3.\left(x+\frac{9}{2}\right)^2+\frac{1}{4}}\)

để B lớn nhất => \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\)nhỏ nhất

mà \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\)vì \(3.\left(x+\frac{3}{2}\right)^2\ge0\)

dấu = xảy ra khi \(x+\frac{3}{2}=0\)

=> x=\(-\frac{3}{2}\)

Vậy maxB=\(41\)khi x=\(-\frac{3}{2}\)

3) \(M=\frac{3x^2+14}{x^2+4}=\frac{3.\left(x^2+4\right)+2}{x^2+4}=3+\frac{2}{x^2+4}\)

để M lớn nhất => x²+4 nhỏ nhất

mà \(x^2+4\ge4\)(vì x² lớn hơn hoặc bằng 0)

dấu = xảy ra khi x² =0

=> x=0

Vậy Max M\(=\frac{7}{2}\)khi x=0

ps: bài này khá dài, sai sót bỏ qua =))

ê viết lộn dòng này :v

\(MinA=\frac{2017}{2018}\)nha 

Thanks. <3

A=[2(x^2-8x+22)-1]/(x^2-8x+22)

A=2-1/[(x-4)^2+6]

A nho nhat khi (x-4)^2=0=> x=4

min(A)=2-1/6

`I=3x-9x^{2}-1`

`I=-(9x^2-3x+1)`

`I=-(9x^2-3x+1/4+3/4)`

`I=-(3x-1/2)^{2}-3/4`

Vì `-(3x-1/2)^2 <= 0` với mọi `x`

  `=>-(3x-1/2)^2-3/4 <= -3/4` với mọi `x`

  Hay `I <= -3/4` với mọi `x`

   `=>I_{mi n}=-3/4 <=>x=1/6`

a: \(A=-4x^2+4x-1\)

\(=-\left(4x^2-4x+1\right)\)

\(=-\left(2x-1\right)^2\le0\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

b: \(B=-x^2+5x\)

\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}\right)+\dfrac{25}{4}\)

\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\forall x\)

Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)

a) \(A=-4x^2+4x-1=-\left(4x^2-4x+1\right)\)

\(=-\left(2x-1\right)^2\le0\)

\(maxA=0\Leftrightarrow x=\dfrac{1}{2}\)

b) \(B=-x^2+5x=-\left(x^2-5x+\dfrac{25}{4}\right)+\dfrac{25}{4}\)

\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)

\(maxB=\dfrac{25}{4}\Leftrightarrow x=\dfrac{5}{2}\)

c) \(C=-3x^2-9x+6=-3\left(x^2+3x+\dfrac{9}{4}\right)+\dfrac{51}{4}\)

\(=-3\left(x+\dfrac{3}{2}\right)^2+\dfrac{51}{4}\le\dfrac{51}{4}\)

\(maxC=\dfrac{51}{4}\Leftrightarrow x=-\dfrac{3}{2}\)

Thử tất cả với x = 0                 

A = -3x^2 - 6x = -3( x^2 + 2x ) = - 3 ( x^2 + 2x + 1 - 1 ) = - 3 [ ( x+ 1 )^2 - 1 )

= - 3( x + 1 )^2 + 3

Vì -3(x + 1 )^2 <=0 => -3( x+ 1 )^2 + 3 <= 3 

VẬy GTLN của A là 3 khi x+  1 = 0 => x = -1

B = 2x - x^2 

  = - ( x^2 -2x )

 = - ( x^2 -2x+  1 - 1 )

= - [ ( x- 1 )^2 - 1 )

= - ( x-  1 )^2 + 1 

Vì  - ( x-  1 )^2 <= 0 => - ( x - 1 )^2 + 1 <= 1 

VẬy GTLN của B = 1 khi x = 1 

C = 12x - 9x^2 + 15

  = - ( 9x^2 -12x + 15)

 = - (9x^2 - 2.3x.2 + 4 + 9 )

 = - ( 3x- 2 )^2 - 9 

Đánh giá tương Tự 

VẬy GTLN B = -9 khi x =2/3 

Đúng cho mình nha 

Chọn A