Cho hình bình hành ABCD có CD + AD = 16, AB - BC = 8. Tính tỉ số \(\dfrac{AB}{BC}\).

Những câu hỏi liên quan
Cho hình bình hành ABCD có CD + AD = 16, AB - BC = 8. Tính tỉ số \(\dfrac{AB}{BC}\).
ta có: Hình bình hành ABCD
`=>` AB=CD;AD=BC
xét: CD +AD =16 (mà CD = AB)
`=>` AB+AD=16 (1)
AB -BC =8 (mà BC =AD)
`=>` AB- AD =8 (2)
Lấy (1) `+` (2) vế theo vế ta có:
(AB -BC) + (AB - AD) =16 +8
`=>` 2 AB= 24
`=>` AB= 12
`=>` AD=BC=16-12=4
`=>` tỉ số :`(AB)/(BC) = 12/4 =3`
Đúng 1
Bình luận (0)
Cho tứ giác \(ABCD\) , gọi \(M,N,P,Q\) lần lượt là trung điểm của \(AB,BC,CD,DA\). Biết \(MP=\dfrac{1}{2}\left(AD+BC\right)\), \(NQ=\dfrac{1}{2}\left(AB+CD\right)\). \(CMR:\) tứ giác \(ABCD\) là hình bình hành.
Trên tia đối của PB lấy H sao cho BP = PH
ΔBPC và ΔHPD có:
BP = HP (cách vẽ)
\(\widehat{BPC}=\widehat{HPD}\left(đối.đỉnh\right)\) (đối đỉnh)
PC = PD (gt)
Do đó, ΔBPC=ΔHPD(c.g.c)
=> BC = DH (2 cạnh t/ứng)
và \(\widehat{PBC}=\widehat{PHD}\) (2 góc t/ứ), mà 2 góc này ở vị trí so le trong nên BC // HD
ΔABH có: M là trung điểm của AB (gt)
P là trung điểm của BH (vì HP = BP)
Do đó MP là đường trung bình của ΔABH
\(\Rightarrow MP=\dfrac{1}{2}AH\) ; MP // AH
\(\Rightarrow2MP=AH\)
Có: \(AD+DH\ge AH\) (quan hệ giữa 3 điểm bất kì)
\(\Leftrightarrow AD+BC\ge2MP\) (thay \(DH=BC;AH=2MP\))
\(\Leftrightarrow\dfrac{AD+BC}{2}\ge MP\)
Mà theo đề bài: \(MP=\dfrac{BC+AD}{2}\)
Do đó, \(AD+DH=AH\)
=> A,D,H thẳng hàng
Mà HD // BC (cmt) nên AD // BC
Tương tự: AB // CD
Tứ giác ABCD có: AD // BC (cmt);AB // CD (cmt)
Do đó, ABCD là hình bình hành
Đúng 2
Bình luận (0)
Cho tứ giác ABCD có: AB=5cm; AB+BC=12cm; BC+CD=12cm; CD+AD=12cm. CM: tứ giác ABCD là hình bình hành
helpp
AB = 5cm
=> BC = 12 - 5 = 7cm
=> CD = 12 - 7 = 5cm
=> AD = 12 - 5 = 7cm
Vì AB = CD, BC = AD, mà AB đối CD, BC đối AD
=> Tứ giác ABCD là hbh
Đúng 0
Bình luận (0)
cho hình bình hành ABCD biết AB=CD, CD>AB và AD=AB=BC. Góc BDC=30 độ. Tính các góc ngoài của hình thang
Tứ giác ABCD là hình bình hành nếu:
A. AB = CD;
B. AD = BC;
C. AB // CD và AD = BC;
D. AB = CD và AD = BC.
Hãy chọn phương án đúng.
Cho hình thang ABCD có: AB // CD, AB = 4, CD = 16, AC = 8, AD = 12. Độ dài BC là:
A. 8
B. 13
C. 12
D. 6
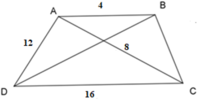
Ta có:
A B A C = 4 8 = 1 2 , A C C D = 8 16 = 1 2 ⇒ A B A C = A C C D = 1 2
Xét ΔABC và ΔCAD có:
A B A C = A C C D (cmt)
B A C ^ = A C D ^ (cặp góc so le trong)
=> ΔABC ~ ΔCAD (c - g - c)
⇒ A B A C = C A C D = B C A D = 1 2 ⇒ B C 12 = 1 2 ⇒ x = 12.1 2 = 6
Đáp án: D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có ADC+BCD=90° và AD=BC . Gọi M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD. a) Chúng minh rằng tứ giác MNPQ là hình bình hành. b) đường thẳng PM cắt BC tại E. tính góc PEC. c) chứng minh diện tích MNPQ≥ (AB-CD)²/8. đẳng thức xảy ra khi nào?
PLEASE!❤️🙏
Hình thang ABCD có đáy AB, CD.
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
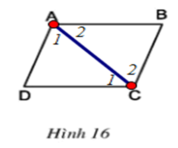
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
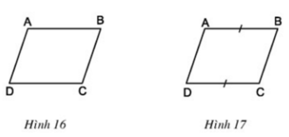
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
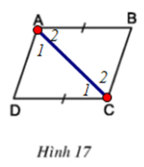
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD có AB = 12 cm, BC = 8 cm, AH = 6 cm (AH là đường cao ứng với cạnh CD). Tính chu vi và diện tích của hình bình hành ABCD
Chu vi hình bình hành ABCD là:
\(\left(12+8\right)\times2=40\left(cm\right)\)
Diện tích hình bình hành ABCD là:
\(12\times6=72\left(cm^2\right)\)
Giải
Chu vi hình bình hành ABCD đó là :
\(\left(12+8\right)\times2=40\) ( cm )
Diện tích hình bình hành ABCD đó là :
\(12\times6=72\)( cm2 )
Đáp số : Chu vi : \(40\)cm ; Diện tích : \(72\)cm2


















