Số sản phẩm một công nhân làm được trong một ngày được cho như sau:
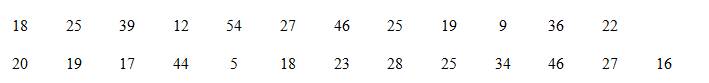
Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sau nhóm có độ dài bằng nhau.
Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:
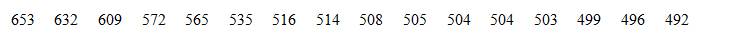
(Theo: https://www.premierleague.com/)
Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau
Tham khảo:
Giá trị lớn nhất là: 653.
Giá trị bé nhất là: 492.
Khoảng biến thiên là: 653 - 492 = 161.
Để chia thành 7 nhóm có độ dài bằng nhau, ta lấy điểm đầu mút trái của nhóm đầu tiên là 492, điểm đầu mút phải của nhóm cuối là 653 với độ dài mỗi nhóm là 23.
Ta có mẫu số liệu ghép nhóm sau:

Cân nặng (kg) của 35 người trưởng thành tại một khu dân cư được cho như sau:

Chuyển mẫu số liệu trên thành dạng ghép nhóm, các nhóm có độ dài bằng nhau, trong đó có nhóm [40; 45)
Ba nhóm công nhân có tổng cộng là 63 người. Trong 1 ngày, mỗi công nhân đội 1 lầm được 6 sản phẩm; mỗi công nhân đội 2 làm được 5 sản phẩm ; mỗi công nhân đội 3 làm được 3 sản phẩm . Tính số công nhân mỗi đội, biết số sản phẩm mỗi đội làm trong 1 ngày là bằng nhau
Số sản phẩm mỗi đội bằng nhau => số công nhân sẽ theo như sau:
Đội 1 mỗi người làm được 6 sản phẩm/ngày nên số công nhân đội 1 là 5 phần bằng nhau.
Đội 2 mỗi người làm được 5 sản phẩm/ngày nên số công nhân đội 2 là 6 phần bằng nhau.
Đội 3 mỗi người làm được 3 sản phẩm/ngày nên số công nhân đội 2 là 10 phần bằng nhau.
Giá trị 1 phần là : 63 : (5+6+10) = 3 (người)
Số công nhân đội 1 là : 3.5=15(người)
Số công nhân đội 2 là : 3.6=18(người)
Số công nhân đội 3 là : 3.10=30(người)
Đáp số : ...
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:

Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:

Hai nhóm công nhân cùng nhau đi đào mương và đào xong cùng một lúc. Nhóm công thứ nhất đào được 20m mương trong một ngày, nhóm công nhân thứ hai đào được 25m mương trong một ngày. Nhóm công nhân thứ hai làm sau nhóm công nhân thứ nhất 15 ngày và đào được số mét mương bằng 1/2 số mét mương nhóm công nhân thứ nhất đào được. Hỏi cả hai nhóm công nhân đào được tất cả bao nhiêu mét mương?
Hai nhóm công nhân cùng nhau đi đào mương và đào xong cùng một lúc. Nhóm công thứ nhất đào được 20m mương trong một ngày, nhóm công nhân thứ hai đào được 25m mương trong một ngày. Nhóm công nhân thứ hai làm sau nhóm công nhân thứ nhất 15 ngày và đào được số mét mương bằng \(\frac{1}{2}\) số mét mương nhóm công nhân thứ nhất đào được. Hỏi cả hai nhóm công nhân đào được tất cả bao nhiêu mét mương?
Một nhóm có 3 người làm trong 5 ngày được 30 sản phẩm . Hỏi nếu nhóm có 7 người trong 4 ngày thì làm bao nhiêu sản phẩm ? ( Mức làm của mỗi người như nhau ) ( Giải bằng 2 cách )
1 người làm 5 ngày được số sản phẩm là :
30 : 3 = 10 ( sản phẩm )
1 người 1 ngày được số sản phẩm là :
10 : 5 = 2 ( sản phẩm )
7 người 1 ngày được số sản phẩm là :
2 x 7 = 14 ( sản phẩm )
7 người 4 ngày được số sản phẩm là :
14 x 4 = 56 ( sản phẩm )
Đáp số : 56 sản phẩm
1 người làm 5 ngày được số sản phẩm là :
30 : 3 = 10 ( sản phẩm )
1 người 1 ngày được số sản phẩm là :
10 : 5 = 2 ( sản phẩm )
7 người 1 ngày được số sản phẩm là :
2 x 7 = 14 ( sản phẩm )
7 người 4 ngày được số sản phẩm là :
14 x 4 = 56 ( sản phẩm )
Đáp số : 56 sản phẩm
Đề bài
Một thư viện thống kê số lượng sách được mượn mỗi ngày trong ba tháng ở bảng sau:

Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Tham khảo:
Do số quyển sách là số nguyên nên ta hiệu chỉnh lại như sau:

Số sách trung bình được mượn mỗi ngày sau khi ghép nhóm là:
\(\bar x = \frac{{3.18 + 6.23 + 15.28 + 27.33 + 22.38 + 14.43 + 5.48}}{{92}} \approx 34,6\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {30,5;35,5} \right)\).
Do đó: \({u_m} = 30,5;{n_{m - 1}} = 15;{n_m} = 27;{n_{m + 1}} = 22;{u_{m + 1}} - {u_m} = 35,5 - 30,5 = 5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 30,5 + \frac{{27 - 15}}{{\left( {27 - 15} \right) + \left( {27 - 22} \right)}}.5 \approx 34\)
Vậy số lượng sách được mượn mỗi ngày cao nhất là 35 quyển.
Quãng đường (km) từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:

a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là \(\left[ {0;5} \right)\). Tìm giá trị đại diện cho mỗi nhóm
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
Tham khảo:
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 6 + 7.5 \times 10 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.5\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chưa mốt là \(\left[ {10;15} \right)\).