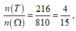Tìm các tam giác cân trong Hình 11 và đánh dấu vào các cạnh bằng nhau.
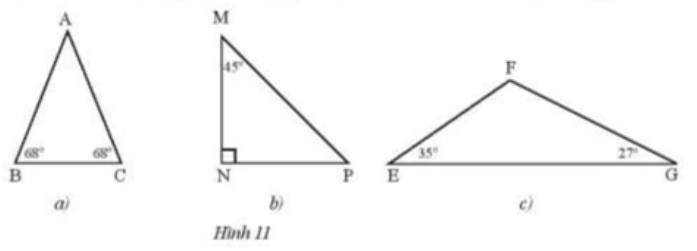
Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.
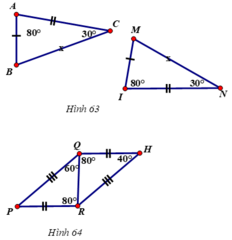
- Xem hình 63)
Ta có:
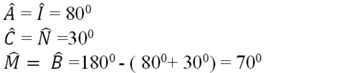
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
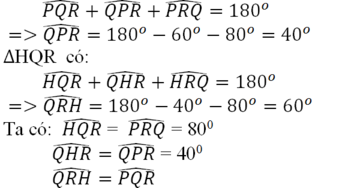
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
tìm trong các hình 63, 64 ( SGK Toán/111) các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bỏi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó.
làm gấp nha ngày 3/11/2016 mình phải nộp rùi
ai làm nhanh nhất và đúng nhất mình sẽ tick 1 cái và kết bạn lun!
Tìm trong các hình 63, 64 các tam giác bằng nhau (các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó ? Viết kí hiệu về sự bằng nhau của các tam giác đó ?

Xem hình a) ta có:
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Xem hình a) ta có:
ˆAA^=ˆII^=800,ˆCC^=ˆNN^=300
ˆBB^=ˆMM^=1800-(800+300)=700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
ˆQ2Q2^=ˆR2R2^=800 (ở vị trí so le trong)
Nên QH// RP
Nên ˆR1R1^ = ˆQ1Q1^= 600(so le trong)
ˆPP^=ˆHH^= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Cho hình 61 Hai tam giác ABC và MNP có bằng nhau hay không (Các cạnh hoặc các góc bằng nhau được đánh dấu bằng những kí hiệu giống nhau) ?
Nếu có, hãy viết kí hiệu về sự bằng nhau của hai tam giác đó
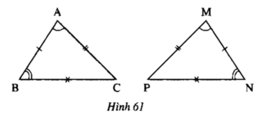
Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP
quan sát hình 60a và 60b các cạnh bằng nhau được đánh dấu bởi các kí hiệu giống nhau. Viết kí hiệu thể hiện sự bằng nhau của hai tam giác có trên hình đó
Cho mình hỏi hình ở đâu ak
Ko có hình ko làm đc đâu
Hai tam giác ABC và MNP có bằng nhau hay ko (các cạnh hoặc các góc bằng nhau được đánh dấu bởi những kí hiệu giống nhau) ?
nếu có, hãy viết kí hiệu về sự bằng nhau của hai tam giác đó
b) Hãy tìm:
Đỉnh tương ứng với góc N, cạnh tương ứng với cạnh AC
c) Điền vào chỗ trống (...) tam giácABC=..., AC=..., góc B=...,
Quan sát hình 60a và 60b, các cạnh bằng nhau được đánh dấu bởi các kí hiệu giống nhau. Viết kí hiệu thể hiện sự bằng nhau của 2 tam giác có trên hình đó.(sách lớp 7 vnen trang 140)
Tìm trong các hình 63, 64 các tam giác bằng nhau ( các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau ). Kể tên các đỉnh tương ứng của các tam giác bằng nhau đó. Viết kí hiệu về sự bằng nhau của các tam giác đó .
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ
hinh 63
dinh A = dinh I
dinh C = dinh N
dinh B = dinh M
\(\Rightarrow\)tam giac \(ABC=\)tam giac \(IMN\)
hinh 64
dinh P = dinh H
dinh chua goc \(\widehat{PQR}=\)dinh chua goc \(\widehat{QRH}\)
dinh chua goc \(\widehat{PRQ}=\)dinh cua goc \(\widehat{RQH}\)
\(\Rightarrow\)tam giac \(PQR=\)tam giac \(HRQ\)
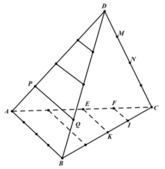
Cho hình tứ diện đều ABCD. Trên mỗi cạnh của tứ diện, ta đánh dấu 3 điểm chia đều cạnh tương ứng thành các phần bằng nhau. Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu. Lấy ra từ S một tam giác, xác suất để mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho bằng
A . 2 45
B . 9 34
C . 2 5
D . 4 15
Chọn D
Cách 1:
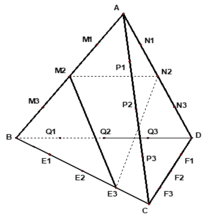
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
![]()
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
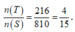
Cách 2: Lưu Thêm
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có ![]()
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy