Tìm số đo x của \(\widehat {uOt}\) trong Hình 12.
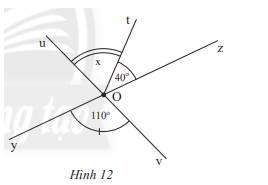
Quan sát hình 12:
a) Tìm góc đối đỉnh của \(\widehat {yOv}\)
b) Tính số đo của \(\widehat {uOz}\)
a) Góc đối đỉnh của \(\widehat {yOv}\) là \(\widehat {zOu}\) vì tia Oz đối tia Oy, Ou đối tia Ov
b) Ta có: \(\widehat {uOz} = \widehat {yOv}\) ( 2 góc đối đỉnh), mà \(\widehat {yOv} = 110^\circ \) nên \(\widehat {uOz} = 110^\circ \)
Quan sát hình 5.
a) Tìm các góc kề với \(\widehat {tOz}\)
b) Tìm số đo của góc kề bù với \(\widehat {mOn}\).
c) Tìm số đo của \(\widehat {nOy}\)
d) Tìm số đo của góc kề bù với \(\widehat {tOz}\).
a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)
b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)
c) Ta có:
\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {nOy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy \(\widehat {nOy} = 60^\circ \)
d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

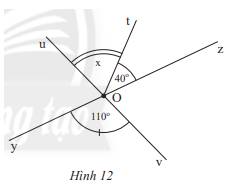
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).
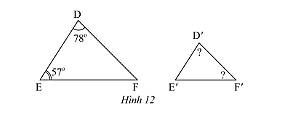
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
Trong Hình 30, tính số đo của \(\widehat {mOp};\widehat {qOr};\widehat {pOq}\)
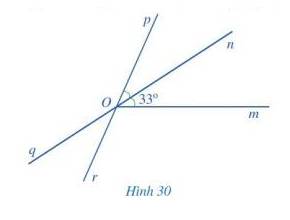
Vì On là tia phân giác của \(\widehat {mOp}\) nên:
+) \(\widehat {pOn}= \widehat {mOn}=33^\circ \)
+) \(\widehat {mOp} = 2.\widehat {mOn} = 2.33^\circ = 66^\circ \)
Vì \(\widehat {qOr} = \widehat {pOn}\) ( 2 góc đối đỉnh), mà \(\widehat {pOn} = 33^\circ \Rightarrow \widehat {qOr} = 33^\circ \)
Vì \(\widehat {pOq} + \widehat {qOr} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {pOq} + 33^\circ = 180^\circ \Rightarrow \widehat {pOq} = 180^\circ - 33^\circ = 147^\circ \)
Vậy \(\widehat {mOp} = 66^\circ ;\widehat {qOr} = 33^\circ ;\widehat {pOq} = 147^\circ \)
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
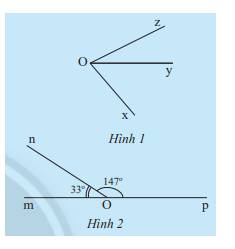
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
Quan sát Hình 14.
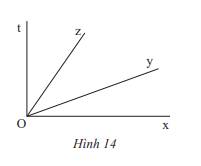
a) Tìm các góc kề với \(\widehat {xOy}\).
b) Tìm số đo của \(\widehat {tOz}\) nếu cho biết \(\widehat {xOy} = 20^\circ ;\widehat {xOt} = 90^\circ ;\widehat {yOz} = \widehat {tOz}\).
a) Các góc kề với \(\widehat {xOy}\) là: \(\widehat {yOz};\widehat {yOt}\)
b) Ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\\ \Rightarrow 20^\circ + \widehat {zOt} + \widehat {zOt} = 90^\circ \\ \Rightarrow 2.\widehat {zOt} = 90^\circ - 20^\circ = 70^\circ \\ \Rightarrow \widehat {zOt} = 70^\circ :2 = 35^\circ \end{array}\)
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).

Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)
Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat A\),\(\widehat B\),\(\widehat C\),\(\widehat D\).
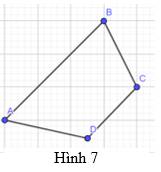
Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC
\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC = \({180^o}\)
\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\)