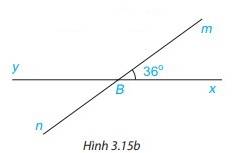
Cho Hình 3.15b, biết \(\widehat {xBm} = 36^\circ \). Tính số đo các góc còn lại trong hình vừa vẽ.
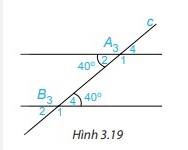
a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.
b) Các cặp góc A1 và B4; A2 và B3 được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)
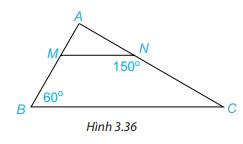
1. Cho Hình 3.36, biết MN//BC, \(\widehat {ABC} = 60^\circ ,\widehat {MNC} = 150^\circ \).
Hãy tính số đo các góc BMN và ACB.
2. Cho Hình 3.37, biết rằng xx’//yy’ và zz’ \( \bot \) xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không?

1. Vì MN//BC nên \(\widehat {AMN} = \widehat {ABC}\)( 2 góc đồng vị), mà \(\widehat {ABC} = 60^\circ \)nên \(\widehat {AMN} = 60^\circ \)
Vì \(\widehat {AMN} + \widehat {BMN} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {BMN} = 180^\circ \\ \Rightarrow \widehat {BMN} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
Vì \(\widehat {ANM} + \widehat {MNC} = 180^\circ \)(2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {ANM} + 150^\circ = 180^\circ \\ \Rightarrow \widehat {ANM} = 180^\circ - 150^\circ = 30^\circ \end{array}\)
Vì MN//BC nên \(\widehat {ANM} = \widehat {ACB}\) ( 2 góc đồng vị), mà \(\widehat {ANM} = 30^\circ \)nên \(\widehat {ACB} = 30^\circ \).
2. Vì xx’//yy’ nên \(\widehat {x'AB} = \widehat {ABy}\)( 2 góc so le trong)
Mà zz’\( \bot \) xx’ nên \(\widehat {x'AB} = 90^\circ \)
Do đó, \(\widehat {ABy} = 90^\circ \) nên zz’ vuông góc với yy’.
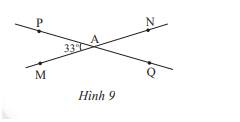
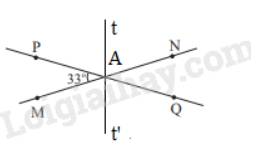
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành \(\widehat {PAM} = 33^\circ \) (Hình 9)
a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của \(\widehat {PAN}\). Hãy tính số đo của \(\widehat {tAQ}\). Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của \(\widehat {MAQ}\)
a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau
Cho Hình 3.42, biết rằng Ax//Dy, \(\widehat A = 90^\circ ,\widehat {BCy} = 50^\circ \). Tính số đo các góc ADC và ABC.

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó, \(\widehat{ADC}=90^0\)
Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Vậy \(\widehat{ADC}=90^0; \widehat {ABC} = 50^\circ \)
Cho đoạn thẳng AB. Vẽ hai tia Ax, By sao cho chúng tạo với AB hai góc so le trong có cùng số đo bằng 60\(^\circ \)(\(\widehat {xAB} = \widehat {yBA} = 60^\circ \)). Trên hình vừa vẽ, hai đường thẳng chứa hai tia Ax và By có song song với nhau không? Vì sao?
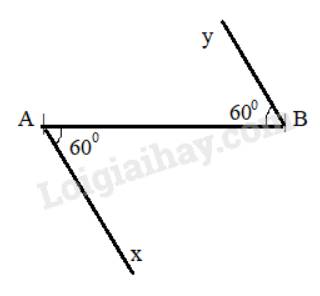
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
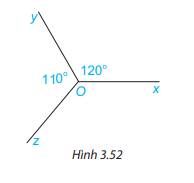
Cho Hình 3.52, biết \(\widehat {xOy} = 120^\circ ,\widehat {yOz} = 110^\circ \). Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia Oy
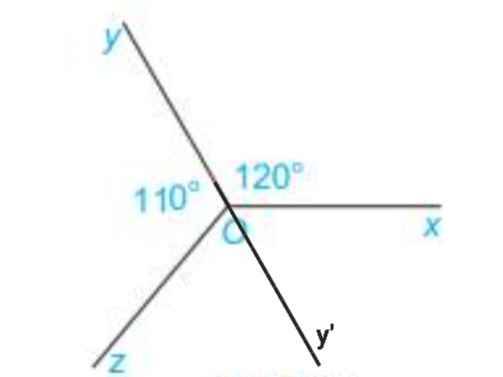 Vẽ tia Oy' là tia đối của tia Oy
Vẽ tia Oy' là tia đối của tia Oy
Ta có:
∠xOy + ∠xOy' = 180⁰ (kề bù)
⇒ ∠xOy' = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰
Lại có:
∠zOy + ∠zOy' = 180⁰ (kề bù)
⇒ ∠zOy' = 180⁰ - ∠zOy
= 180⁰ - 110⁰
= 70⁰
⇒ ∠zOx = ∠zOy' + ∠xOy'
= 70⁰ + 60⁰
= 130⁰
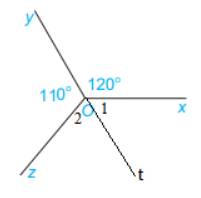
Kẻ Ot là tia đối của tia Oy.
Ta được:+) \(\widehat {{O_1}} + \widehat {xOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{O_1}} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {{O_1}} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
+) \(\widehat {{O_2}} + \widehat {yOz} = 180^\circ \)( 2 góc kề bù)
Vì Ot nằm giữa 2 tia Ox và Oz nên \(\widehat {xOz} = \widehat {{O_1}} + \widehat {{O_2}} = 60^\circ + 70^\circ = 130^\circ \)
Vậy \(\widehat {zOx} = 130^\circ \)
Cho Hình 3.15a, biết \(\widehat {DMA} = 45^\circ \). Tính số đo góc DMB.
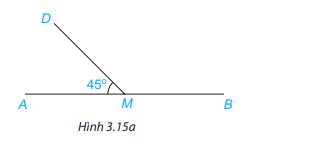
Vì góc AMD và BMD là hai góc kề bù nên
\(\begin{array}{l}\widehat {AMD} + \widehat {BMD} = 180^\circ \\ \Rightarrow 45^\circ + \widehat {BMD} = 180^\circ \\ \Rightarrow \widehat {BMD} = 180^\circ - 45^\circ = 135^\circ \end{array}\)
Vậy \(\widehat {DMB} = 135^\circ \)
Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết \(\widehat {xOz} = 38^\circ \) (hình 6)
Tính số đo các góc \(\widehat {xOt},\widehat {tOy}\) và \(\widehat {yOz}\)
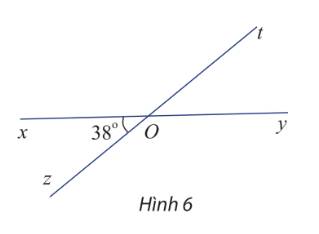
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)
hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)
\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 38^\circ = 142^\circ \)
Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.

Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).