Quan sát Hình 87.
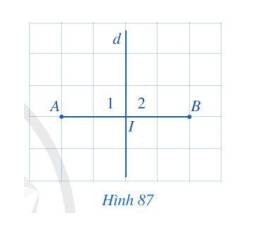
a) So sánh hai đoạn thẳng IA và IB.
b) Tìm số đo của các góc \({I_1},{I_2}\).
Đoạn mạch gồm hai điện trở R1 và R2 mắc song song. Mối quan hệ giữa cường độ dòng điện qua mỗi điện trở và điệnt rở của nó được biểu diễn
A. \(I=\dfrac{I_1+I_2}{2}\) B. \(I=I_1=I_2\) C. \(I=I_1+I_2\) D. \(I=I_1-I_2\)
\(R_1//R_2\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}\)
\(I=I_1+I_2\)
Chọn C.
Quan sát hình 4.3a.
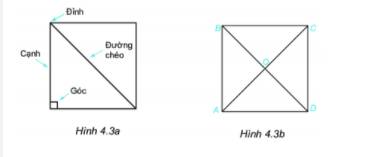
1. Nêu tên các đỉnh, cạnh, đường chéo của hình vuông ABCD (h.4.3b).
2. Dùng thước thẳng đo và so sánh độ dài các cạnh của hình vuông, hai đường chéo của hình vuông.
3. Dùng thước đo góc để đo và so sánh các góc của hình vuông.
1) Các đỉnh: A, B, C, D
Các cạnh: AB, BC, CD, DA
Các đường chéo: AC, BD
2) Độ dài các cạnh của hình vuông đều bằng nhau
Độ dài 2 đường chéo của hình vuông bằng nhau
3) Các góc của hình vuông đều bằng nhau và bằng 90o
Quan sát hình chữ nhật ở hình 4.8a.
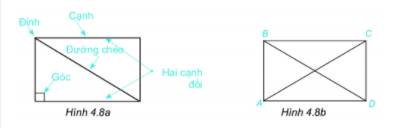
1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (h.4.8b).
2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.
3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.
Quan sát Hình 10.
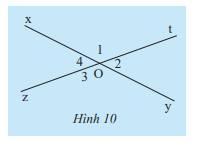
a) Hãy dùng thước đo góc để đo \(\widehat {{O_1}}\)và \(\widehat {{O_3}}\). So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). So sánh số đo hai góc đó.
Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)
Cho hai dòng điện thẳng dài, song song, cùng chiều.I_1= 12 A, I_2, = 8 A. Gọi M là điểm nằm ở khoảng giữa hai dòng điện, cách dòng điện I_1, một đoạn bằng 0,2 m, cách dòng điện I_2, một đoạn bằng 0,4 m.
a. Vẽ hình biểu diễn các vectơ cảm ứng từ do hai dòng điện trên gây ra tại M. b. Xác định cảm ứng từ tổng hợp tại M
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
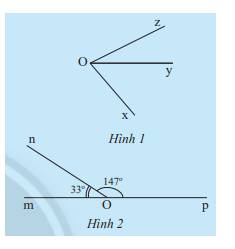
a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)
Quan sát Hình 3.
a) So sánh hệ số góc của hai đường thẳng:
\(d:y = 2x + 3\) và \(d':y = 2x - 2\).
Nêu nhận xét về vị trí giữa hai đường thẳng này.
b) Tìm đường thẳng \(d''\) đi qua gốc tọa độ \(O\) và song song với đường thẳng \(d\).
a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).
Quan sát hình bình hành ở hình 4.12a.
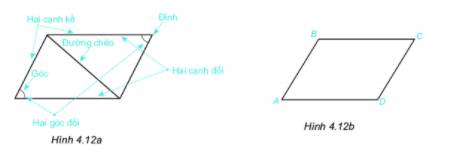
1. Dùng thước thẳng đo và so sánh độ dài các cạnh đổi của hình bình hành ABCD (1.4.12b).
2. Các góc đối của hình bình hành ABCD có bằng nhau không?
3. Các cạnh đối của hình bình hành ABCD có song song với nhau không?
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
Quan sát góc vuông xOy và tia Oz ở Hình 25.
a) Mỗi điểm M (M khác O) thuộc tia Oz có phải là điểm trong của góc xOy hay không? Tia Oz có nằm trong góc xOy hay không?
b) Tính số đo góc yOz.
c) So sánh hai góc xOz và yOz.
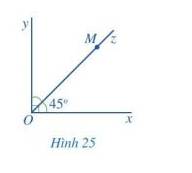
a) Mỗi điểm M (M khác O) thuộc tia Oz đều là điểm trong của góc xOy. Tia Oz có nằm trong góc xOy
b) Vì Oz có nằm trong góc xOy nên
\(\begin{array}{l}\widehat {yOz} + \widehat {zOx} = \widehat {xOy}\\ \Rightarrow \widehat {yOz} + 45^\circ = 90^\circ \\ \Rightarrow \widehat {yOz} = 90^\circ - 45^\circ = 45^\circ \end{array}\)
Vậy số đo góc yOz là 45 độ
c) \(\widehat {xOz} = \widehat {yOz}\) (cùng bằng \(45^o\))