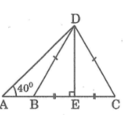
tam giác bcd đều có cạnh 5cm ,góc A = 40 độ tính ab ad

Những câu hỏi liên quan
Cho tam giác BCD đều cạnh 5cm, trên tia đối của tia BC lấy điểm A sao cho góc BAD = 40 độ. Tính AD, AB, S tam giac ADC
Tính AD và AB, biết tam giác BCD là tam giác đều, cạnh 5cm A B C D 40
Đọc tiếp
Tính AD và AB, biết tam giác BCD là tam giác đều, cạnh 5cm
góc ABD=180-60=120 độ
góc BDA=180-120-40=20 độ
Xét ΔBAD có AB/sinADB=BD/sinA=AD/sinDBA
=>AB/sin20=5/sin40=AD/sin120
=>\(AB\simeq2,66\left(cm\right);AD\simeq6,74\left(cm\right)\)
Đúng 1
Bình luận (0)
Kẻ DH vuông góc BC. Tính được DH= \(\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Và BH=HC=5/2 (cm)
\(DH=AD.sinA\Rightarrow AD=\dfrac{5\sqrt{3}}{sin40}\) (bấm máy)
AH= CĂN AD^2-DH^2=> AB=AH-BH=AH-5/2(đoạn này bạn tự tính nha)
Đúng 0
Bình luận (0)
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AD
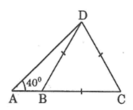
cho tam giác BCD là tam giác đều cạnh 5cm và góc DAB bằng 40o. hãy tính AD và AB
Đọc tiếp
cho tam giác BCD là tam giác đều cạnh 5cm và góc DAB bằng 40o. hãy tính AD và AB
Cho tam giác ABD là tam giác đều cạnh 5cm và góc DAB = 40 độ . Tính
a, AD
b, AB
tam giác đều thì mỗi góc phải bằng 60o chứ
Đúng 0
Bình luận (0)
Cho hình bên. BCD là tam giác đều cạnh 5cm và góc DAB bằng 40 ° . Hãy tính: AB
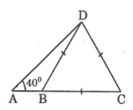
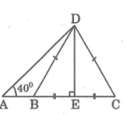
Trong tam giác vuông ADE, ta có:
AE = AD.cotgA ≈ 6,736.cotg 40 °
= 5,16 (cm)
Ta có: AB = AE – BE = 5,16 – 2,5 = 2,66 (cm)
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD) có góc DAB bằng góc DBC AB=3cm AD=3,5cm BD=5cm a) chứng minh tam giác ADB đồng dạng với tam giác BCD b) tính độ dài BC và CD ( làm tròn đến số thập phân số 2) C) tính diện tích tam giác BCD biết diênn tính tam giác ABC là 5,2 cm2
a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: Ta có: ΔADB\(\sim\)ΔBCD
nên DB/CD=AB/BD=AD/BC
=>5/CD=3/5=3,5/BC
=>CD=25/3(cm); BC=35/6(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC và 1 điểm D trên cạnh AB sao cho D không trùng với A vào B.
a) Tính AB biết AD=5cm,BD=6cm
b)tính số đo góc C của tam giác biết ACD=30 độ,BCD=70 độ
Cho hình thang ABCD (AB//CD), biết AB =2,5 cm ,AD=3,5 cm , BD =5cm và góc DAB=DBC.
a)Chứng minh 2 tam giác ADB và BCD đồng dạng .
b)Tính độ dài các cạnh BC và CD
c) Tính tỉ số diện tích 2 tam giác ADB và BCD