Cho hình bình hành abcd. Điểm E thuộc cạnh BC, điểm F thuộc cạnh AB sao cho AE=CF. Gọi H là chân đường vuông góc kẻ từ D xuống CF. Chứng minh rằng DH = DK

Những câu hỏi liên quan
Cho hình bình hành ABCD có điểm E thuộc cạnh BC , điểm G thuộc cạnh AB và AE = CG . Gọi H là chân đường vuông góc kẻ từ D đến AE , K là chân đường vuông góc kẻ từ D đến CG . So sánh độ dài DH và DK
a)Cho hình bình hành ABCD có điểm E thuộc cạnh BC, điểm G thuộc cạnh AB và AE=CG. gọi H là chân đường vuông góc kẻ từ D đến AE, K là chân đường vuông góc kẻ từ D đến CG. Biết DH=5cm. Tính DK
b)Cho tam giác đều ABC. Diểm I thuộc cạnh AB, điểm K thuộc cạnh AC, BK và CI cắt nhau tại E. Biết diện tích tứ giác AIEK bằng diện tích tam giác BEC. chứng tỏ rằng BI=AK
BẠN GỬI HÌNH ĐC KO
Hello bạn Bảo thân mến có cần mik bảo thầy giúp ko
Đúng 2
Bình luận (0)
cho hình bình hành ABCD gọi E,F,G,H lần luợt là điểm thuộc AB,CD,BC,AD sao cho AE=CF,BG=DH chứng minh rằng tứ giác EGFH là hình bình hành( vẽ hình) giúp vs ạ
Ta có: AE+EB=AB
CF+FD=CD
mà AB=CD
và AE=CF
nên EB=FD
Ta có: AH+HD=AD
CG+BG=CB
mà AD=CB
và HD=BG
nên AH=CG
Xét ΔAHE và ΔCGF có
AH=CG
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔAHE=ΔCGF
Suy ra: HE=GF
Xét ΔEBG và ΔFDH có
EB=FD
\(\widehat{B}=\widehat{D}\)
BG=DH
Do đó: ΔEBG=ΔFDH
Suy ra: EG=FH
Xét tứ giác EHFG có
EG=FH
EH=FG
Do đó: EHFG là hình bình hành
Đúng 0
Bình luận (0)
Hình bình hành ABCD. Gọi E, F, G, H lần lượt là các điểm thuộc cạnh AB, CD, BC, AD sao cho AE=CF, BG=DH. CMR AC, BD, EF, GH đồng quy
Cho hình bình hành ABCD có góc A bằng 60 độ. Lấy các điểm E, F theo thứ tự thuộc các cạnh AD, CD sao cho DE=CF. Gọi K là điểm đối xứng với F qua BC. Chứng minh rằng EK//AB
Cho tam giác ABC cân tại C (AB < AC). Kẻ ba đường cao AD, BE, CF cắt nhau tại H ( D thuộc BC, E thuộc AC, F thuộc AB). Kẻ DM vuông góc CF tại M, DK vuông góc với AC tại K. Gọi N là giao điểm của EF với tia CB. Chứng minh: CE.CN = FE.FN + CF^2
Cho tam giác ABC cân tại C (AB < AC). Kẻ ba đường cao AD, BE, CF cắt nhau tại H ( D thuộc BC, E thuộc AC, F thuộc AB). Kẻ DM vuông góc CF tại M, DK vuông góc với AC tại K. Gọi N là giao điểm của EF với tia CB. Chứng minh: CE.CN = FE.FN + CF^2
cho hình bình hành abcd trên cạnh ab lấy điểm e trên cạnh dc lấy điểm f sao cho ae bằng cf trên cạnh ad lấy điểm h trên cạnh bc lấy điểm g sao cho dh bằng bc
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng : CE = CF
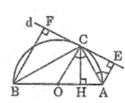
Ta có: OC ⊥ d (tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF (tính chất đường thẳng song song cách đều)
Đúng 0
Bình luận (0)














