\(x\left(3x-2\right)-3x^2=\dfrac{3}{4}\)

\(\Leftrightarrow3x^2-2x-3x^2=\dfrac{3}{4}\)

\(\Leftrightarrow-2x=\dfrac{3}{4}\)

\(\Leftrightarrow x=\dfrac{3}{4}:\left(-2\right)\)

\(\Leftrightarrow x=-\dfrac{3}{8}\)

\(P=\dfrac{x^4+x^3-3x-1}{x^2+x+1}=\dfrac{\left(x^2-1\right)\left(x^2+x+1\right)-2x}{x^2+x+1}=x^2-1-\dfrac{2x}{x^2+x+1}\)

Vì x \(\in Z\) nên để P \(\in Z\) thì : \(\dfrac{x}{x^2+x+1}\in Z\) 

Đặt \(A=\dfrac{x}{x^2+x+1}\) . Với x = 0 ; ta có : \(P=-1\in Z\)

Với x khác 0 ; ta có : \(A=\dfrac{1}{x+\dfrac{1}{x}+1}\)

Nếu x > 0 ; ta có : \(0< A\le\dfrac{1}{3}\) ( vì \(x+\dfrac{1}{x}\ge2\) )  => Ko tồn tại g/t nguyên của A (L) 

Nếu x < 0 ; ta có : \(x+\dfrac{1}{x}\le-2\)  \(\Rightarrow x+\dfrac{1}{x}+1\le-1\) 

Suy ra : \(0>A\ge\dfrac{1}{-1}=-1\)  \(\Rightarrow A=-1\) 

" = " \(\Leftrightarrow x+\dfrac{1}{x}=-2\Leftrightarrow x=-1\)

x = -1 ; ta có : P = 2 \(\in Z\) (t/m) 

Vậy ... 

\(x^2-2xy+y^2+3x-3y-4=0\)

\(\Leftrightarrow\left(x-y\right)^2+3\left(x-y\right)-4=0\)

\(\Leftrightarrow\left(x-y\right)\left(x-y+3\right)-4=0\)

Thay y = 3 vào biểu thức trên ta được : 

\(x\left(x-3\right)-4=0\)

\(\Leftrightarrow x^2-3x-4=0\Leftrightarrow\left(x-4\right)\left(x+1\right)=0\Leftrightarrow x=4;x=-1\)

Vậy với y = 3 thì x = 4 ; x = -1 

Thay y = 3 vào bthuc ta được :

x² - 6x + 9 + 3x - 9 - 4 = 0

<=> x² - 3x - 4 = 0

<=> ( x + 1 )( x - 4 ) = 0

<=> x = -1 hoặc x = 4 

Đáp án: B

Với  x ≥ 0 , x ≠ 25  Ta có:  A = B . x − 4

⇔ x + 2 x − 5 = 1 x − 5 . x − 4 ⇔ x + 2 = x − 4 ( * )

Nếu  x ≥ 4 ,   x ≠ 25  thì (*) trở thành : x + 2 = x − 4

⇔ x − x − 6 = 0 ⇔ x − 3 x + 2 = 0

Do  x + 2 > 0  nên  x = 3 ⇔ x =   9  (thỏa mãn)

Nếu  0 ≤ x < 4  thì (*) trở thành : x + 2 = 4 − x

⇔ x + x − 2 = 0 ⇔ x − 1 x + 2 = 0

Do  x + 2 > 0  nên  x = 1 ⇔ x = 1  (thỏa mãn)

Vậy có hai giá trị x=1 và x= 9 thỏa mãn yêu cầu bài toán

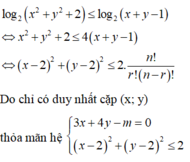
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)² + (y – 2)² = 2.

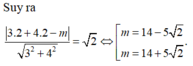
Chọn C.