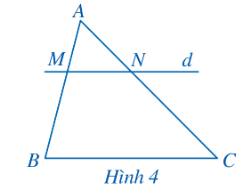
Trong Hình 4, chứng tỏ rằng nếu \(MN\parallel BC\) thì \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\).
cho tam giác ABC , trên AB lấy điểm M sao cho AM = MB .trên AC lấy điểm N sao cho AN = 2 NC . Đường thẳng MN cắt BC kéo dài tại D. chứng tỏ rằng BC =CD
Trên các cạnh của AC,AB của tam giác ABC lần lượt lấy N,M sao cho \(\frac{AM}{MB}\)= \(\frac{AN}{NC}\). Chứng minh MN//BC.
Xét tg ABC có \(\frac{AM}{MB}=\frac{AN}{NC}\) => MN // BC ( Áp dụng đl TL đảo)
Cho một hình chữ nhật ABCD. Trên AB lấy điểm M sao cho AM = MB, lấy điểm N trên BC sao cho BN gấp đôi NC. Hãy chứng tỏ rằng diện tích hình tam giác AMN bằng \(\frac{1}{6}\)diện tích hình chữ nhật ABCD.
Ta có: \(S_{AMN}=\frac{BN.AM}{2}=\frac{BN\cdot\frac{1}{2}AB}{2}\)
\(S_{ABN}=\frac{AB.BN}{2}\)
=> \(\frac{S_{AMN}}{S_{ABN}}=\frac{\frac{\frac{1}{2}BN.AB}{2}}{\frac{AB.BN}{2}}=\frac{1}{2}\) => \(S_{AMN}=\frac{1}{2}S_{ABN}\)(1)
Ta lại có: BN = 2NC; BN + NC = BC => BN = 2/3BC
\(S_{ABN}=\frac{AB.BN}{2}=\frac{AB\cdot\frac{2}{3}BC}{2}\)
\(S_{ABCD}=AB.BC\)
\(\frac{S_{ABN}}{S_{ABCD}}=\frac{\frac{\frac{2}{3}AB.BC}{2}}{AB.BC}=\frac{1}{3}\) => \(S_{ABN}=\frac{1}{3}S_{ABCD}\) => \(\frac{1}{2}S_{ABN}=\frac{1}{6}S_{ABCD}\)(2)
Từ (1) và (2) => \(S_{AMN}=\frac{1}{6}S_{ABCD}\)
awbb ưieaaaaaaaa
r
ewfrsd
tf
sdfdyufee
e
ẻ
r
re
ê
r
e
ẻ
e
re
ẻ
rr
cho tam giác ABC, MN song song với BC(M,N lần lượt thuộc AB,AC)
aC/m \(\frac{AM}{AB}=\frac{AN}{AC}\)
b,\(\frac{AM}{MB}=\frac{AN}{NC}\)
Chứng minh định lí Thales thì dùng diện tích nha bạn.
Cụ thể như sau:
Vẽ \(MH,NK\) vuông góc \(BC\) thì thấy ngay \(S\left(BMC\right)=S\left(BNC\right)\) (\(S\) là diện tích hình)
Suy ra \(S\left(AMC\right)=S\left(ANB\right)\) hay \(\frac{S\left(AMC\right)}{S\left(ABC\right)}=\frac{S\left(ANB\right)}{S\left(ACB\right)}\), nghĩa là có câu a.
Mà có câu a thì có câu b
Chứng tỏ rằng nếu abc=1 thì\(\frac{a}{ab+a+1}\)+\(\frac{b}{bc+b+1}\)+\(\frac{c}{ac+c+1}\)=1
Cho tam giác ABC.Trên cạnh AB lấy điểm M sao cho MB=MA,trên cạnh AC lấy điểm N sao cho NC =1/2 NA.Đường thẳng MN cắt cạnh BC kéo dài tại D.
a)So sánh diện tích 2 hình tam giác AMN và BMN.
b)So sánh diện tích 2 hình AMN và BMNC.
c)Chứng tỏ rằng BC=CD.
a)\(\Delta AMN,\Delta BMN\)có chung đường cao hạ từ N,có đáy AM = BM nên SAMN = SBMN
b) AC = AN + NC = AN +\(\frac{1}{2}AN=\frac{3}{2}AN\)nên\(\Delta ABC,\Delta ABN\)có chung đường cao hạ từ B ; đáy AC = 3/2 AN
\(\Rightarrow S_{ABC}=\frac{3}{2}S_{ABN}=\frac{3}{2}\left(S_{AMN}+S_{BMN}\right)=\frac{3}{2}\times2S_{AMN}=3S_{AMN}\)
\(\Rightarrow S_{MNCB}=S_{ABC}-S_{AMN}=3S_{AMN}-S_{AMN}=2S_{AMN}\Rightarrow S_{AMN}=\frac{1}{2}S_{MNCB}\)
c)\(\Delta AMD,\Delta BMD\)có chung đường cao hạ từ D ; đáy AM = MB nên SAMD = SBMD mà SAMN = SBMN
=> SAMD - SAMN = SBMD - SBMN => SAND = SBND mà \(\Delta NCD,\Delta AND\)có chung đường cao hạ từ D ; đáy NC = 1/2 AN
=> SNCD = 1/2 SAND = 1/2 SBND mà\(\Delta NCD,\Delta BND\)có chung đường cao hạ từ N nên có đáy CD = 1/2 BD
=> BC = CD
Cho tam giác ABC.Trên cạnh AB lấy điểm M sao cho MB=MA,trên cạnh AC lấy điểm N sao cho NC =1/2 NA.Đường thẳng MN cắt cạnh BC kéo dài tại D.
a)So sánh diện tích 2 hình tam giác AMN và BMN.
b)So sánh diện tích 2 hình AMN và BMNC.
c)Chứng tỏ rằng BC=CD.
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
a) Vì \(d\parallel CD\) nên \(MP\parallel CD\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{MD}} = \frac{{AP}}{{PC}}\,\,\left( 1 \right)\) (Định lý Thales)
Vì \(d\parallel AB\) nên \(PN\parallel AB\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{BN}}{{NC}} = \frac{{AP}}{{PC}}\,\,\left( 2 \right)\) (Định lý Thales)
Từ (1) và (2) ta có \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\).
b) Vì \(MD = 2MA\) nên \(\frac{{AM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{AD}} = \frac{{MP}}{{DC}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{MP}}{{DC}} = \frac{1}{3} \Rightarrow MP = \frac{1}{3}DC = 2cm\)
Vì \(\frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{CA}} = \frac{2}{3}\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{CP}}{{CA}} = \frac{{PN}}{{AB}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{PN}}{{AB}} = \frac{2}{3} \Rightarrow PN = \frac{2}{3}AB = \frac{8}{3}cm\)
Mà \(MN = MP + PM = 2 + \frac{8}{3} = \frac{{14}}{3}cm\).
Cho ΔABC có BC = a. Trên cạnh AB lấy điểm M sao cho MB =\(\frac{1}{4}\)AB. Trên cạnh AC lấy điểm N sao cho NC = \(\frac{1}{4}\)AC. Tính MN theo a .
Ai giúp e vs ạ, 3 **** luôn nak