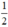a: Khi m=-2 thì phương trình sẽ là \(x^2-8x-9=0\)

=>(x-9)(x+1)=0

=>x=9 hoặc x=-1

b: \(\text{Δ}=\left(4m\right)^2-4\left(4m-1\right)\)

\(=16m^2-16m+4=\left(4m-2\right)^2>=0\)

Để phương trình có hai nghiệm phân biệt thì 4m-2<>0

hay m<>1/2

`a)` Thay `m=-2` vào ptr có:

    `x^2+4.(-2)x+4.(-2)-1=0`

`<=>x^2-8x-9=0`

Ptr có: `a-b+c=1-(-8)+(-9)=0`

 `=>x_1=-1;x_2=[-c]/a=9`

Vậy với `m=-2` thì `S={-1;9}`

_____________________________________________

`b)` Ptr có `2` nghiệm pb

`<=>\Delta' > 0`

`<=>(2m)^2-(4m-1) > 0`

`<=>4m^2-4m+1 > 0`

`<=>(2m-1)^2 > 0`

   `=>(2m-1)^2 \ne 0`

`<=>2m-1 \ne 0<=>m \ne 1/2`

Vậy ...........

a) Với m=-2, phương trình đã cho trở thành x²-8x-9=0. Do 1-(-8)+(-9)=0 nên phương trình có hai nghiệm x₁=-1 và x₂=9.

b) Để phương trình đã cho có hai nghiệm phân biệt thì \(\Delta\)'=(2m)²-(4m-1)>0, suy ra x\(\ne\dfrac{1}{2}\).

a) Để phương trình trên là phương trình bậc nhất thì: m≠\(\dfrac{3}{8}\)

c) Để phương trình vô nghiệm thì: m=0

d) Để phương trình vô số nghiệm thì m=\(\dfrac{3}{8}\)

a/ \(\left(2m-3\right)x+\left(x-3\right)4m+2mx=0\)

\(\Leftrightarrow\left(8m-3\right)x-12m=0\)

Để phương trình là hàm số bậc 1 :

\(8m-3\ne0\Leftrightarrow m\ne\dfrac{3}{8}\)

b/ Phương trình vô nghiệm :

\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m\ne0\end{matrix}\right.\)

c/ Phương trình vô số nghiệm khi :

\(\Leftrightarrow\left\{{}\begin{matrix}8m-3=0\\12m=0\end{matrix}\right.\)

(2m-3)x+(x-3)4m+2mx=0

=>(2m-3)x+4mx-12m+2mx=0

=>x(2m-3+4m+2m)-12m=0

=>-3x-12m=0

a: Để phương trình là phương trình bậc nhất thì 2m-3-4m+2m<>0

hay \(m\in R\)

b: Để phương trình vô nghiệm thì \(m\in\varnothing\)

(m+1) x 2 +4mx+4m -1 =0     (2)

Ta có:  ∆ ' = 2 m 2  – (m +1)(4m -1) = 4 m 2  – 4 m 2  + m – 4m +1

= 1 – 3m

Phương trình (2) có 2 nghiệm phân biệt khi và chỉ khi:

*m +1 ≠ 0 ⇔ m  ≠  -1

và * ∆ ' > 0 ⇔ 1 -3m > 0 ⇔ 3m < 1 ⇔ m < 1/3

Vậy m < 1/3 và m  ≠  -1 thì phương trình đã cho có 2 nghiệm phân biệt

b > Để pt 1 có 2 nghiệm phân biệt 

=> \(\Delta>0\)  <=> \(3^2-4\left(m-3\right)>0\)

<=> 9 -4m +12 >0 

<=> -4m+21>0

<=> m<\(\dfrac{21}{4}\)

Vậy m<\(\dfrac{21}{4}\)  là giá trị cần tìm tm yc đề bài

phần a tự giải nha bạn

Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 

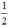
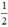
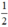
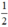Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < ; có nghiệm kép khi m =  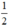và vô nghiệm khi m >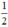 

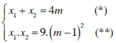
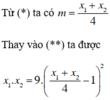
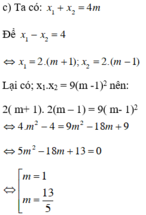
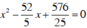a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)

Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9

Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0

⇔ -5m2 + 18m – 9 ≥ 0

⇔ 5m2 - 18m + 9 ≤ 0

⇔ (5m – 3)(m – 3) ≤ 0

⇔ 3/5 ≤ m ≤ 3.

b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:

+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.

Thử lại:

+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4

+ m = 13/5, (1) trở thành  có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.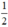

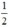
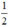
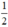Vậy m = 1 hoặc m = 13/5.

a) Phương trình  x 2   –   2 ( m   –   1 ) x   +   m 2   =   0  (1)

Có a = 1; b’ = -(m – 1);  c   =   m 2

b) Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 

Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < ; có nghiệm kép khi m =  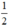và vô nghiệm khi m > 

a/ Xét pt :

\(x^2-2\left(m-1\right)+2m-5=0\)

\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)

\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m

b/ Phương trình cớ 2 nghiệm trái dấu

\(\Leftrightarrow2m-5< 0\)

\(\Leftrightarrow m< \dfrac{5}{2}\)

c/ Theo định lí Vi - et ta có :

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)

\(A=x_1^2+x_2^2\)

\(=\left(x_1+x_2\right)^2-2x_1.x_2\)

\(=4\left(m-1\right)^2-2\left(2m-5\right)\)

\(=4m^2-8m+4-4m+10\)

\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)

\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)

1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)

Vậy pt luôn có 2 nghiệm pb với mọi m 

2, Vì pt có 2 nghiệm trái dấu 

\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)

3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)

\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)

\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)

\(=\left(2m-3\right)^2+6\ge6\forall m\)

Dấu ''='' xảy ra khi m = 3/2 

Vậy với m = 3/2 thì A đạt GTNN tại 6 

1: \(\text{Δ}=\left(2m-2\right)^2-4\left(2m-5\right)\)

\(=4m^2-8m+4-8m+20\)

\(=4m^2-16m+24\)

\(=4m^2-16m+16+8\)

\(=\left(2m-4\right)^2+8>0\forall m\)

Do đó: Phương trình luôn có hai nghiệm phân biệt

2: Để phương trình có hai nghiệm trái dấu thì 2m-5<0

hay m<5/2

3: \(A=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=\left(2m-2\right)^2-2\left(2m-5\right)\)

\(=4m^2-8m+4-4m+10\)

\(=4m^2-12m+14\)

\(=4m^2-12m+9+5\)

\(=\left(2m-3\right)^2+5\ge5\forall m\)

Dấu '=' xảy ra khi m=3/2