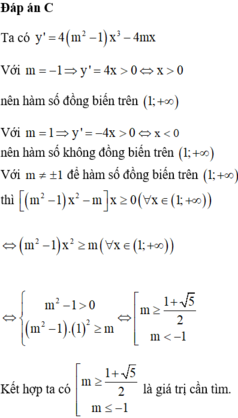Tìm các khoảng đồng biến của hàm số: y = 2sinx + cos2x, x ∈ [0;π] A. (0; pi/2 B. (pi/2; pi) C. (0; pi/6) và pi/2; 5pi/6) D. (0;pi).

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để hàm số
y
(
m
2
-
1
)
x
4
-
2
m
x
2
đồng biến trên khoảng
(
1
;
+
∞
)
A.
m
≤
-
1
B. m -1 hoặc
m
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = ( m 2 - 1 ) x 4 - 2 m x 2 đồng biến trên khoảng ( 1 ; + ∞ )
A. m ≤ - 1
B. m = -1 hoặc m > 1 + 5 2
C. m ≤ - 1 hoặc m ≥ 1 + 5 2
D. m ≤ - 1 hoặc m > 1
Tìm khoảng đồng biến của hàm số
y
-
x
3
+
3
x
2
-
2
Đọc tiếp
Tìm khoảng đồng biến của hàm số y = - x 3 + 3 x 2 - 2
![]()
![]()
![]()
![]()
Tìm m để hàm số y = 1 3 x 3 - x 2 - m x + 1 luôn đồng biến trên từng khoảng xác định của nó
A. m < - 1
B. m > -1
C. m ≤ -1
D. m > -1
Để hàm số
,
y
-
x
3
3
+
a
-
1
x
2
+
a
+
3
x...
Đọc tiếp
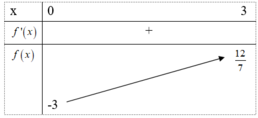
Để hàm số , y = - x 3 3 + a - 1 x 2 + a + 3 x - 4 đồng biến trên khoảng 0 ; 3 thì giá trị cần tìm của tham số a là:
A. a < - 3
B. a > - 3
C. - 3 < a < 12 7
D. a ≥ 12 7
Cho hàm số yf(x) có bảng biến thiên như hình.Hàm số đã cho đồng biến trên khoảng A.
-
∞
;
-
1
B. (-1;3) C. (-3;0) D.
(
0
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình.
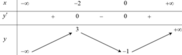
Hàm số đã cho đồng biến trên khoảng
A. - ∞ ; - 1
B. (-1;3)
C. (-3;0)
D. ( 0 ; + ∞ )
Cho hàm số yf(x) có bảng biến thiên như hìnhHàm số đã cho đồng biến trên khoảng A.
-
∞
;
-
1
B.
-
1
;
3
C.
-
3
;
0
D. ...
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình
![]()
Hàm số đã cho đồng biến trên khoảng
A. - ∞ ; - 1
B. - 1 ; 3
C. - 3 ; 0
D. 0 ; + ∞
Đáp án B
Từ bảng xét dấu f'(x) ta thấy trên khoảng ( - ∞ ; - 1 ) thì f'(x)<0 nên hàm số y=f(x) nghịch biến trên khoảng ( - ∞ ; - 1 )
Đúng 0
Bình luận (0)
cho ham số bật nhất y=(2m-3)x+5. Tìm các giá trị cua m hàm số
a/ Đồng biến
b/ Nghịch biến
Chú ý ; Hàm số có dạng y = ax + b (a khác 0) đồng biến khi a > 0 , nghịch biến khi a < 0
Vậy :
a/ Hàm số đồng biến khi 2m-3 > 0 => m > 3/2
b/ Hàm số nghịch biến khi 2m-3 < 0 => m < 3/2
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
m
2
-
1
x
+
2
m
-
3
.Tất cả các giá trị của tham số m để hàm số đồng biến trên
ℝ
là A.
m
3
2
B. -1 m 1 C.
[
m...
Đọc tiếp
Cho hàm số y = f x = m 2 - 1 x + 2 m - 3 .
Tất cả các giá trị của tham số m để hàm số đồng biến trên ℝ là
A. m > 3 2
B. -1 < m < 1
C. [ m < - 1 m > 1
D. m ≠ ± 1
Hàm số y = ax + b ( a ≠ 0 ) đồng biến trên R khi a> 0.
Do đó, để hàm số đã cho đồng biến trên R thì m 2 - 1 > 0 ⇔ [ m > 1 m < - 1
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số y = x 3 - 6 x 2 + 9 x + 7 . Hàm số đồng biến trên khoảng
A. (1; 3)
B. (1; +∞)
C. (-∞; 3)
D. (-∞; 1) và (3; +∞)