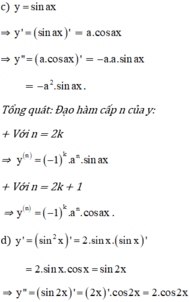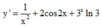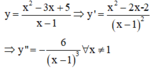Tìm đạo hàm cấp hai của hàm số \(y = \sin 3x\)
Những câu hỏi liên quan
Tính đạo hàm cấp hai của các hàm số sau: y = sin a x
Tìm đạo hàm của hàm số:
y
2
x
2
-
1
x
+
sin
2
x
+
3
x
+
1
A.
y
4
x
-
1
x
2
+
c
o
s
2
x
+
3...
Đọc tiếp
Tìm đạo hàm của hàm số: y = 2 x 2 - 1 x + sin 2 x + 3 x + 1
A. y ' = 4 x - 1 x 2 + c o s 2 x + 3 x ln 3
B. y ' = 4 x + 1 x 2 + c o s 2 x + 3 x ln 3
C. y ' = 4 x + 1 x 2 + c o s 2 x + 3 x ln 3
D. y ' = 2 x + 1 x 2 + c o s 2 x + 3 x
SGK Cánh Diều
13 tháng 8 2023 lúc 22:35
Tìm đạo hàm của mỗi hàm số sau:
a) \(y = \sin 3x + {\sin ^2}x\)
b) \(y = {\log _2}(2x + 1) + {3^{ - 2x + 1}}\)
a: \(y'=\left(sin3x\right)'+\left(sin^2x\right)'=3\cdot cos3x+sin\left(x+pi\right)\)
b: \(y'=\left(log_2\left(2x+1\right)\right)'+\left(3^{-2x+1}\right)'\)
\(=\dfrac{2}{\left(2n+1\right)\cdot ln2}-2\cdot3^{-2x+1}\cdot ln3\)
Đúng 1
Bình luận (0)
Đạo hàm cấp hai của hàm số
y
x
2
−
3
x
+
5
x
−
1
A.
x
2
−
2
x
−
2...
Đọc tiếp
Đạo hàm cấp hai của hàm số y = x 2 − 3 x + 5 x − 1
A. x 2 − 2 x − 2 x − 1 2
B. 6 x − 1 3
C. − 6 x − 1 3
D. x 2 − x − 2 x − 1 2
Tìm đạo hàm cấp hai của hàm số sau :
\(y=x^2\sin x\)
\(y'\left(x\right)=\left(x^2\right)'sinx+x^2.\left(sinx\right)'\)\(=2x.sinx+x^2.cosx\)
\(y''\left(x\right)=\left[2x.sinx+x^2.cosx\right]'\)\(=\left(2xsinx\right)'\)\(+\left(x^2.cosx\right)'\)
\(=2sinx+2xcosx+2x.cosx+x^2.\left(-sinx\right)\)\(=2sinx+4x.cosx-x^2sinx\).
Đúng 0
Bình luận (0)
Tìm đạo hàm cấp hai của hàm số sau :
\(y=\sin x\sin2x\sin3x\)
Tính đạo hàm của hàm số y=sin 2x + 3 x
Tính đạo hàm của hàm số
y
sin
2
x
+
3
x
A.
y
2
cos
2
x
+
x
.
3
x
-
1
B.
y
-
cos
2
x
+
3
x...
Đọc tiếp
Tính đạo hàm của hàm số y = sin 2 x + 3 x
A. y ' = 2 cos 2 x + x . 3 x - 1
B. y ' = - cos 2 x + 3 x
C. y ' = - 2 cos 2 x - 3 x ln 3
D. y ' = 2 cos 2 x + 3 x ln 3
Tìm đạo hàm cấp hai của hàm số sau: y = xcos2x