cho (O) và một đường thẳng d năm ngoài. P chuyển động trên d. Qua P kẻ hai tiếp tuyến PA, PB tới (O). gọi I là hình chiếu của O lên d. Từ I kẻ hai tiếp tuyến IM, IM tới (O). MN cắt OI tại H.
a) CMR: A, H, B thẳng hàng

Những câu hỏi liên quan
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.2. Giả sử AI AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI? 3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID IC thì AB luôn đi qu...
Đọc tiếp
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID > IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.
2. Giả sử AI = AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI?
3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID > IC thì AB luôn đi qua một điểm cố định.
1) Trong (O) có CD là dây cung không đi qua (O) và H là trung điểm CD
\(\Rightarrow OH\bot CD\Rightarrow\angle OHI=90=\angle OAI\Rightarrow OHAI\) nội tiếp
Ta có: \(\angle OAI+\angle OBI=90+90=180\Rightarrow OAIB\) nội tiếp
\(\Rightarrow O,H,A,B,I\) cùng thuộc 1 đường tròn
2) Vì IA,IB là tiếp tuyến \(\Rightarrow IB=IA=OA=OB\Rightarrow AOBI\) là hình thoi
có \(\angle OAI=90\Rightarrow AOBI\) là hình vuông
AB cắt OI tại E.Dễ chứng minh được E là trung điểm AB
Ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{2}R\Rightarrow AE=\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) bán kính của (AOBI) là \(\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) diện tích của (AOBI) là \(\left(\dfrac{\sqrt{2}}{2}R\right)^2.\pi=\dfrac{1}{2}\pi R^2\)
3) OH cắt AB tại F
Ta có: \(\angle IEF=\angle IHF=90\Rightarrow IEHF\) nội tiếp
\(\Rightarrow OH.OF=OE.OI\) (cái này chỉ là đồng dạng thôi,bạn tự chứng minh nha)
mà \(OE.OI=OB^2=R^2\Rightarrow OF=\dfrac{R^2}{OH}\)
mà H cố định \(\Rightarrow\) F cố định \(\Rightarrow AB\) đi qua điểm F cố định 
Đúng 0
Bình luận (0)
cho(O;R) và điểm I sao cho IO =2R . một đường thẳng d đi qua I cắt (O;R) tại 2 điểm A,B phân biệt. từ I kẻ 2 tiếp tuyến IM,IN tới (O;R). gọi H là trung điểm của AB và J,K là giao điểm của MN với IO,IH
a) chứng minh 4 điểm O,H,M,N cùng nằm trên 1 đường tròn
b)chứng minh IK.IH=IJ.IO
c)tính diện tích tam giác IMN theo R
a: ΔOAB cân tại O
mà OH là trung tuyến
nên OH vuông góc AB
góc OHI=góc OMI=góc ONI=90 độ
=>O,H,M,I,N cùng thuộc đường tròn đường kính OI
=>ĐPCM
b: Xét (O) co
IM,IN là trung tuyến
=>IM=IN
mà OM=ON
nên OI là trung trực của MN
=>OI vuông góc MN tại J
Xet ΔIJK và ΔIHO có
góc IJK=góc IHO
góc JIK chung
=>ΔIJK đồng dạng với ΔIHO
=>IJ/IH=IK/IO
=>IK*IH=IJ*IO
c: sin MIO=OM/OI=1/2
=>góc MIO=30 độ
=>góc MIN=60 độ
\(IM=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(S_{IMN}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3\cdot R^2\cdot\sqrt{3}}{4}\)
Đúng 0
Bình luận (0)
Cho đường tròn (O) và một điểm I nằm ngoài đường tròn. Qua I kẻ hai tiếp tuyến IM và IN với đường tròn (O). Gọi K là điểm đối xứng với M qua O. Đường thẳng IK cắt đường tròn (O) tại H.
a) Chứng minh tứ giác IMON nội tiếp.
b) Chứng minh tam giác INH đồng dạng tam giác IKN và IN^2=IH.IK
c) chứng minh HM.KN=HN.KM
giúp mình ý b,c
a: góc IMO+góc INO=180 độ
=>IMON nội tiếp
b: Xét ΔINH và ΔIKN có
góc INH=góc IKN
góc NIH chung
=>ΔINH đồng dạng với ΔIKN
=>IN^2=IH*IK
Đúng 0
Bình luận (1)
Cho đường tròn (O) và một điểm I nằm ngoài đường tròn. Qua I kẻ hai tiếp tuyến IM và IN với đường tròn (O). Gọi K là điểm đối xứng với M qua O. Đường thẳng IK cắt đường tròn (O) tại H.
a) Chứng minh tứ giác IMON nội tiếp.
b) Chứng minh tam giác INH đồng dạng tam giác IKN và IN^2=IH.IK
c) chứng minh HM.KN=HN.KM
giúp mình ý b,c
Cho đường tròn (O;R)và điểm A cố định ngoài đg tròn .qua A kẻ hai tiếp tuyến AM . AN tới đg tròn (M.N là hai tiếp điểm ). Một đường thẳng d đi qua A cắt đg tròn (O;R)tại B và C(AB<AC) Gọi I là trung điểm BC . Đường thẳng qua B song song AM cắt MN tại E
a. Cmr IE song song MC
Ta có : góc AMO = góc ANO = 900 (t/c tiếp tuyến)
Mặt khác I là tđ BC => OI vuông góc BC (t/c đường kính và dây) => góc AIO = 900
=> 5 điểm A, M, O, I, N cùng nằm trên một đường tròn
Ta có góc MAI = góc MNI (AMIN nt), mà góc EBI = góc MAI (đồng vị, do AM // BE) => góc MNI = góc EBI hay góc ENI = góc EBI
=> Tứ giác NBEI nội tiếp => góc BNE = góc BIE. Mà góc BNE = góc BCM (cùng chắn cung MB trong (O))
=> góc BIE = góc BCM => IE // CM
Đúng 0
Bình luận (0)
Cho đường tròn O bán kính R và một điểm P nằm bên ngoài đường tròn . Kẻ các tiếp tuyến PA ,PB với đường tròn ( O , R ) ( A, B là hai tiếp điểm ). Gọi C là điểm đối cứng của B qua O . Đường thẳng OC cắt đường tròn ( O ,R ) tại điểm D ( khác C) . Hai đường thẳng AD và OP cắt nhau tại Q a, Chứng minh tứ giác PAOB nội tiếp đường tròn b, Chứng mình rằng PQ mũ 2 QA*QD c, Giả sử P cách O một khoảng 4 căn 3 cm. Tính bán kính R của đường tròn đã cho để tứ giác OAQB là hình thoi.
Đọc tiếp
Cho đường tròn O bán kính R và một điểm P nằm bên ngoài đường tròn . Kẻ các tiếp tuyến PA ,PB với đường tròn ( O , R ) ( A, B là hai tiếp điểm ). Gọi C là điểm đối cứng của B qua O . Đường thẳng OC cắt đường tròn ( O ,R ) tại điểm D ( khác C) . Hai đường thẳng AD và OP cắt nhau tại Q a, Chứng minh tứ giác PAOB nội tiếp đường tròn b, Chứng mình rằng PQ mũ 2 = QA*QD c, Giả sử P cách O một khoảng 4 căn 3 cm. Tính bán kính R của đường tròn đã cho để tứ giác OAQB là hình thoi.
cho đường tròn (o) đường kính AB và đường thẳng d là tiếp tuyến của đường tròn kẻ từ B. trên d lấy hai điểm nằm khác phía với điểm B và BCBD.AC cắt (o) tại E, AD cắt (o) tại F.(E,F khác A) đường thẳng kẻ qua A vuông góc với EF cắt CD tại M.a) chứng minh tứ giác CEFD nội tiếp.b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CEFD. chứng minh IM vuông góc với CD.c) gọi P là giao điểm của FE và CD. PA cắt đường tròn (o) tại K (K khác A) c/m K,B,I thẳng hàng
Đọc tiếp
cho đường tròn (o) đường kính AB và đường thẳng d là tiếp tuyến của đường tròn kẻ từ B. trên d lấy hai điểm nằm khác phía với điểm B và BC<BD.AC cắt (o) tại E, AD cắt (o) tại F.(E,F khác A) đường thẳng kẻ qua A vuông góc với EF cắt CD tại M.
a) chứng minh tứ giác CEFD nội tiếp.
b) Gọi I là tâm đường tròn ngoại tiếp tứ giác CEFD. chứng minh IM vuông góc với CD.
c) gọi P là giao điểm của FE và CD. PA cắt đường tròn (o) tại K (K khác A) c/m K,B,I thẳng hàng
Cho đường tròn (O;R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thẳng d ở ngoài đường tròn (O) sao chi IDIC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD. a, Chứng minh 5 điểm A, H, O, B, I cùng thuộc 1 đường tròn .b, Giả sử AIAO, khi đó tứ giác AOBI là hình gì ? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI .c, Chứng minh rằng khi điểm I di chuyển trên đường thẳng d thỏa mãn: ở ngoài (O) và IDIC thì AB luôn đi qua một điểm cố định
Đọc tiếp
Cho đường tròn (O;R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thẳng d ở ngoài đường tròn (O) sao chi ID>IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
a, Chứng minh 5 điểm A, H, O, B, I cùng thuộc 1 đường tròn .
b, Giả sử AI=AO, khi đó tứ giác AOBI là hình gì ? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI .
c, Chứng minh rằng khi điểm I di chuyển trên đường thẳng d thỏa mãn: ở ngoài (O) và ID>IC thì AB luôn đi qua một điểm cố định
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Tứ giác AMIN là hình gì? Vì sao?
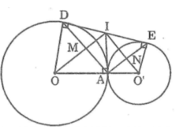
Trong đường tròn (O) ta có OI là tia phân giác của góc AID (tính chất hai tiếp tuyến cắt nhau)
Trong đường tròn (O’) ta có O’I là tia phân giác của góc AIE (tính chất hai tiếp tuyến cắt nhau)
=> IO ⊥ IO’ (tính chất hai góc kề bù)
Suy ra 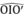 =
90
°
hay
=
90
°
hay  =
90
°
=
90
°
Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác ADI cân tại I
Tam giác cân AID có IO là phân giác của góc AID nên IO cũng là đường cao của tam giác AID
Suy ra: IO ⊥ AD hay 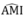 =
90
°
=
90
°
Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AEI cân tại I
Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE
Suy ra: IO’ ⊥ AE hay  =
90
°
=
90
°
Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.
Đúng 0
Bình luận (0)















