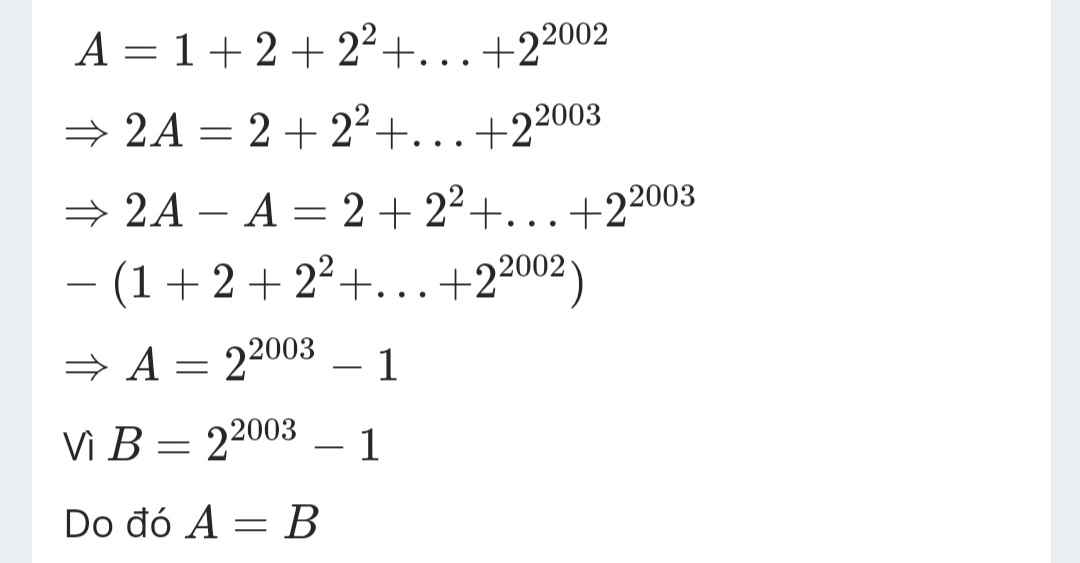2/

A=1+2+2^2+...+2^10

2.A= 2+2^2+...+2^11

=>2A-A = 2^11-1=> A = 2^11 -1=B

Vậy A=B

1)5²⁰⁰³+5²⁰⁰²+5²⁰⁰¹=5²⁰⁰¹(5²+5+1)=5²⁰⁰¹(25+5+1)=5²⁰⁰¹.31

Vì 31 chia hết cho 31nên

5²⁰⁰¹.31chia hết cho 31 hay 5²⁰⁰³+5²⁰⁰²+5²⁰⁰¹ chia hết cho 31

2) A = 1+2+2²+......+2⁹+2¹⁰

=>2A=2+2²+2³+...+2¹¹

=>2A-A=2+2²+2³+...+2¹¹-(1+2+2²+...+2⁹+2¹⁰)

=>A=2¹¹-1

Vậy A=B=2¹¹-1

5^2003+5^2002+5^2001=5^2001(5^2+5+1)=5^2001(25+5+1)=5^2001.31

suy ra:chia hết cho 31

Bạn ơi tại sao bạn lại làm (5²+5+1) vậy.Chỗ đó mik chưa hiểu cho lắm.

Bạn làm ơn có thể giải thích cho mik được không.

A = 1 + 2 + 2² + 2³ + ... + 2²⁰⁰²

=> 2A = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰⁰³

=> 2A - A = ( 2 + 2² + 2³ + 2⁴ + ... + 2²⁰⁰³ ) - ( 1 + 2 + 2² + 2³ + ... + 2²⁰⁰² )

A = 2²⁰⁰³ - 1 < 2²⁰⁰³ 

hay A < B

Vậy ...

\(A=1+2+2^2+2^3+...+2^{2002}\)

\(\Rightarrow2A=2+2^2+2^3+...+2^{2002}+2^{2003}\)

\(\Rightarrow2A-A=2^{2003}-1\)

\(\Rightarrow A=2^{2003}-1\)

Vì \(2^{2003}-1< 2^{2003}\)

nên A < B

Ta có:\(A=1+2+2^2+2^3+...+2^{2002}\)

\(2A=2\left(1+2+2^2+2^3+...+2^{2002}\right)\)

\(2A=2+2^2+2^3+...+2^{2003}\)

\(2A-B=\left(2+2^2+2^3+2^4+...+2^{2003}\right)-2^{2003}\)

\(A-1=2+2^2+2^3+...+2^{2002}\)

\(\Rightarrow A-1=2A-B\)

\(\Rightarrow A>B\)

so sánh 1 và 2 là biết

Ta có \(B=2002^2\)

\(=2002.2002\)

\(=2002.\left(2003-1\right)\)

\(=2002.2003-2002>2003.2002-2003=2001.2003\)

Khi đó A < B 

Vậy....

Mình cảm ơn nha :3

\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)

\(A=1+2+2^2+...+2^{2002}\)

\(2A=2+2^2+2^3+...+2^{2003}\)

\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+...+2^{2002}\right)\)

\(A=2^{2003}-1\)

⇒ \(A=B\)

a, 

A=1+3+3²+3³+3⁴+3⁵+3⁶

=> 3A=3+3²+3³+3⁴+3⁵+3⁶+3⁷

=> 3A-A=(3+3²+3³+3⁴+3⁵+3⁶+3⁷)-(1+3+3²+3³+3⁴+3⁵+3⁶)

=> 2A=3⁷-1

=> A=3⁷-1/2

Vì (3⁷-1)/2   < 3⁷-1 

=> A < B

b, C=1+2+2²+...+2²⁰⁰¹+2²⁰⁰²

=> 2C=2+2²+2³+....+2²⁰⁰²+2²⁰⁰³

=> 2C-C=(2+2²+2³+...+2²⁰⁰²+2²⁰⁰³)-(1+2+2²+...+2²⁰⁰²)

=> C=2²⁰⁰³-1

Vì 2²⁰⁰³-1 = 2²⁰⁰³-1

=> C = D.

a) \(A=1+3+3^2+...+3^6\)

\(\Rightarrow3A=3+3^2+...+3^7\)

\(\Rightarrow3A-A=3+3^2+...+3^7-1-3-3^2-...-3^6\)

\(\Rightarrow2A=3^7+2\)

\(\Rightarrow A=\frac{3^7+2}{2}\)

Vì \(3^7-1>\frac{3^7+2}{2}\)=> A < B.

b) Câu này thì nhân C cho 2 và làm tương tự như câu trên nha.

A=1+3+3^2+3^3+...+3^6

3A=3x(1+3+3^2+3^3+...+3^6)

3A-A=\(\left(3+3^2+3^3+...+3^7\right)-\left(1+3+3^2+...+3^6\right)\)

2A=3^7-1

A= \(\frac{3^7-1}{2}\)

\(\Rightarrow\)A<3^7-1 ( vì  \(\frac{3^7-1}{2}\)  <3^7-1) 

                          ( điều phải chứng minh)

C= 1+2+2^2+...+2^2001+2^2002

2C=2x( 1+2+2^2+...+2^2001+2^2002)

2C-C=(2+2^2+2^3+...+2^2002+2^2003)-( 1+2+2^2+...+2^2001+2^2002)

C=2^2003-1

\(\Rightarrow\)C=2^2003-1

              ( điều phải chứng minh)

bạn ơi bài này là bài toán dạng lũy thừa cơ bản nhất của toán nâng cao lớp 6. bạn học rồi sẽ biết.

A=3+4000=4003

B=4000+2=4002

vì 4003 > 4002 nên A > B

Naruto sai rồi

Như thế này:

A=3+2²+2³+......+2²⁰⁰¹+2²⁰⁰² 

A=1+2²+2³+......+2²⁰⁰¹+2²⁰⁰² 

2A=2.(1+2+2²+2³+......+2²⁰⁰¹+2²⁰⁰² )

2A=1.2+2.2+2²+2³+......+2²⁰⁰¹+2²⁰⁰²)

2A=2+2²+2³+......+2²⁰⁰² +2²⁰⁰³

2A-A=(2+2²+2³+......+2²⁰⁰² +2²⁰⁰³)-(1+2+2²+2³+......+2²⁰⁰¹+2²⁰⁰² )

A=2²⁰⁰³-1

Mà 2²⁰⁰³-1<2²⁰⁰³nên A<B

Nhớ k đúng bạn nhé

A = 1 + 2 + 2² + 2³ + ..... + 2²⁰⁰¹ + 2²⁰⁰² ( đề bài )

2A = 2 . ( 1 + 2 + 2² + 2³ + ....... + 2²⁰⁰¹ + 2²⁰⁰² ) 

2A = 2 + 2² + 2³ + 2⁴ + ....... + 2²⁰⁰² + 2²⁰⁰³

2A - A = ( 1 + 2 + 2² + 2³ + ......+ 2²⁰⁰¹ + 2²⁰⁰² ) - ( 2 + 2² + 2⁴ + ......+ 2²⁰⁰² + 2²⁰⁰³ ) 

 A = 1 + 2²⁰⁰³

mà B = 2²⁰⁰³

\(\Rightarrow\)A > B ( vì 1 + 2²⁰⁰³ > 2²⁰⁰³ )