Tứ giác ABCD có BC=CD và DB là tia phân giác của góc D.Chứng minh rằng ABCD là hình thang
Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. chứng minh rằng ABCD là hình thang
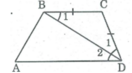
ΔBCD có BC = CD (gt) nên ΔBCD cân tại C.
⇒ ∠ B 1 = ∠ D 1 (tính chất tam giác cân)
Mà ∠ D 1 = ∠ D 2 ( Vì DB là tia phân giác của góc D)
Suy ra: ∠ B 1 = ∠ D 2
Do đó: BC // AD (vì có cặp góc ở vị trí so le trong bằng nhau)
Vậy ABCD là hình thang.
tứ giác ABCD có BC = CD và DB là tia phân giác của góc D . chứng minh rằng ABCD là hình thang
ta có BC = DC (Gt) => tam giác BCD cân tại C => góc CDB = góc CBD (hai góc ở đáy)
mặt khác góc CDB = góc BDA ( vì DB là phân giác góc D)
=> góc CBD = góc BDA (cùng = góc CDB )
mà 2 góc này nằm ở vị trí so le trong nên BC // AD => ABCD là hình thang
tứ giác ABCD có BC=CD và DB là tia phân giác của góc D. chứng minh rằng ABCD là hình thang
ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang
Tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chứng minh rằng ABCD là hình thang ?
Ta có hình vẽ:
Ta có: BC= CD (gt)
=> \(\Delta BCD\) cân tại C
=> góc B1 = góc D1
mà góc D1 = D2 (gt)
=> góc D2 = góc B1
mặt khác 2 góc D2 và B1 đang ở vị trí so le trong
=> AB // CD
=> tứ giác ABCD là hình thang
tứ giác ABCD có BC=CD và DB là tia phân giác của góc D, chứng minh rằng ABCD là hình thang
Vì BC=CD=>Tam giác BCD cân tại C=>\(\widehat{CBD}=\widehat{CDB}\)(1)
Vì DB là tia phân giác của góc D => \(\widehat{CDB}=\widehat{ADB}\)(2)
Từ (1) và (2) => \(\widehat{CBD}=\widehat{ADB}\),mà 2 góc ở vị trí so le trong
=> AD song song với BC.
=> ABCD là hình thang.
Tứ giác ABCD có AB=CD,DB là tia tia phân giác của góc D.Chứng minh ABCD là hình thang
Cho tứ giác ABCD có BC=CD và DB là tia phân giác góc D. Chứng minh rằng ABCD là hình thang
Tứ giác ABCD có BC = CD và DB là tia phân giác D ^ . Chứng minh rằng ABCD là hình thang và chỉ rõ cạnh đáy và cạnh bên của hình thang
Chú ý tam giác CBD cân tại C. Khi đó cùng với DB là phân giác góc S ta chứng minh được A D B ^ = C B D ^
Cho tứ giác ABCD có BC=CD và DB là tia phân giác của D. Chứng minh rằng: ABCD là hình thang