Tam giác ABC vuông ở A,AH vuông góc Bc.
Cho AH = 12,BC=25 tính AB,AC,BH,HC

Những câu hỏi liên quan
cho tam giác abc,kẻ ah vuông góc vs bc,biết ab bằng 15,ah bẳng 12,bc bằng 25,
a) tính bh,hc,ac
b)chứng minh tam giác abc vuông
a. Xét tam giác ABH vuông tại H, theo định lý Py-ta-go ta có:
\(^{AH^2+BH^2=AB^2\Rightarrow12^2+BH^2=15^2\Rightarrow144+BH^2=225}\)
\(\Rightarrow BH^2=225-144\Rightarrow BH^2=81\Rightarrow BH=\sqrt{81}=9\)
Vì H nằm giữa B và C \(\Rightarrow BH+HC=BC\Rightarrow9+HC=25\Rightarrow HC=25-9\Rightarrow HC=16\)
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có:
\(AH^2+HC^2=AC^2\Rightarrow12^2+16^2=AC^2\Rightarrow144+256=AC^2\)
\(\Rightarrow AC^2=400\Rightarrow AC=\sqrt{400}=20\)
Vậy BH = 9, HC = 16 và AC = 20.
- Bạn xem lại câu b nhé :))
Cho tam giác ABC vuông ở A có AC=20cm. Kẻ AH vuông góc BC. Biết BH=9cm;HC=16cm. Tính AB,AH
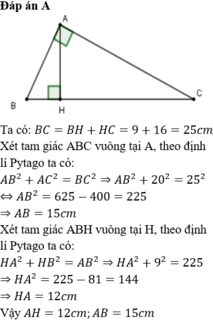
A. AH=12cm;AB=15cm
B. AH=10cm;AB=15cm
C. AH=15cm;AB=12cm
D. AH=12cm;AB=13cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15
Đúng 0
Bình luận (0)
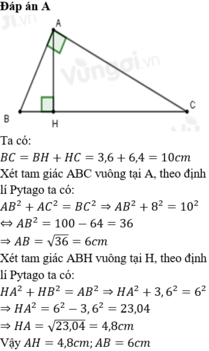
Cho tam giác ABC vuông ở A có AC=8cm. Kẻ AH vuông góc BC. Biết BH=3,6cm;HC=6,4cm. Tính AB,AH
A. AH=4,8cm;AB=6cm
B. AH=8,4cm;AB=6cm
C. AH=4cm;AB=6cm
D. AH=5cm;AB=6cm
Cho tam giác ABC vuông tại A (AB < AC), có đường cao AH. Biết AH = 12 cm, BC = 25 cm. Tính BH, HC, AB, AC (Vẽ hình mẫu)
Sử dụng hệ thức lượng trong tam giác vuông thôi:
AB*AC = AH*BC = 12*25 = 300
AB^2 + AC^2 = BC^2 = 25^2 = 625
giải hệ trên ta được : AB = 15, AC = 20
AB^2 = BH*BC=> BH = AB^2/BC = 9
AH^2 = BH*CH=> CH = AH^2/BH = 12^2/9 = 16
NGOÀI RA HỆ PT TRÊN CÒN 1 NGHIỆM NỮA LÀ AB=20,AC=15
CHo Tam giác ABC, góc A=90, AH vuông góc BC , BH=3,6cm ; HC=6,4cm. Tính BC, AB, AC, AH
Ta có: BC=BH+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=4,8cm\\AB=6cm\\AC=8cm\end{matrix}\right.\)
Đúng 1
Bình luận (0)
BC=BH+HC=3,6+6,4=10CM
AB^2=BH.BC
=>AB=6CM
AC=\(\sqrt{BC^2-AB^2}=8CM\)
AH^2=BH.HC
=>AH=4,8CM
Đúng 1
Bình luận (0)
CHO TAM giác ABC, góc A=90, AK vuông BC,AH=16,BK=25
a tính AB,AC,CK
b AB=12,BK =6.Tính AK,AC,BC,CK
baif2 cho tam giác ABC,AH vuông,AH=3,AC=2
tính AC,HC,AB
cho tam giác ABC vuông cân ở A, biết AB=6cm, AC=8cm, kẻ AH vuông góc với BC tại H. Tính AH, BH và HC
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH24 cm và HC18 cm.
Tính: BH, ,BC,AC,AB và diện tích tam giác ABC
Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB 12 cm và BC20 cm.
Tính: BH, ,AC,HC,AH và diện tích tam giác ABC
Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB3 cm và AC4 cm.
Tính: BH, ,BC,HC,AH và diện tích tam giác ABC
Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC15 cm và AH 12 cm.
Tính: BH, ,BC,A...
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AH=24 cm và HC=18 cm. Tính: BH, ,BC,AC,AB và diện tích tam giác ABC Bài 2: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB= 12 cm và BC=20 cm. Tính: BH, ,AC,HC,AH và diện tích tam giác ABC Bài 3: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=3 cm và AC=4 cm. Tính: BH, ,BC,HC,AH và diện tích tam giác ABC Bài 4: Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AC=15 cm và AH =12 cm. Tính: BH, ,BC,AB,AH và diện tích tam giác ABC Bài 5:Cho tam giác ABC vuông tại A và có đường cao AH. Cho biết AB=20 cm và HC=9cm. Tính: BH, ,BC,AC,AH và diện tích tam giác ABC
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
Đúng 3
Bình luận (0)
cho tam giác ABC có AH Vuông góc với BC , biết AH = 12 cm , BH = 9 cm , AC = 20 cm , AH vuông góc với BC
a/ tính độ dài các đoạn thẳng AB , HC
b/ tam giác ABC là tam giác gì ? vì sao
mong các bạn giúp mk nha mk cảm ơn
a/
∆ABC vuông tại A, AH, vuông góc BC
=> AB.AH = HB.AC
=> AB = 15Ta có: BC^2 = AB^2 + AC^2=> BC = 25=> HB = BC - BH = 25-9 = 16
Đúng 1
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AH^2+BH^2=AB^2\)
\(\Leftrightarrow AB^2=9^2+12^2=225\)
hay AB=15(cm)
Vậy: AB=15cm
Đúng 0
Bình luận (0)