Giúp mik zoi

Những câu hỏi liên quan
Bài 16: Nhà hai bạn Hoa và Lan ở hai bên bờ sông. Nhà bạn Hoa ở địa điểm A, nhà bạn Hoa ở địa điểm B. Bạn Nam muốn sang nhà bạn Lan chơi phải đi đò qua sông, chiếc đò chèo qua sông bị dòng nước đẩy xiên đi một góc 30o và sang đến bờ bên kia tại điểm C. Bạn Hoa phải đi bộ ngược lên một đoạn 200m mới đến nhà bạn Lan. Chiếc đò bị nước đẩy xiên đi phải chèo khoảng bao nhiêu mét mới sang được bờ bên kia? Chiều rộng của khúc sông AB là bao nhiêu?
Đọc tiếp
Bài 16: Nhà hai bạn Hoa và Lan ở hai bên bờ sông. Nhà bạn Hoa ở địa điểm A, nhà bạn Hoa ở địa điểm B. Bạn Nam muốn sang nhà bạn Lan chơi phải đi đò qua sông, chiếc đò chèo qua sông bị dòng nước đẩy xiên đi một góc 30o và sang đến bờ bên kia tại điểm C. Bạn Hoa phải đi bộ ngược lên một đoạn 200m mới đến nhà bạn Lan. Chiếc đò bị nước đẩy xiên đi phải chèo khoảng bao nhiêu mét mới sang được bờ bên kia? Chiều rộng của khúc sông AB là bao nhiêu?
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng A. 60° B.120° C.150° D.135°
Đọc tiếp
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng
A. 60°
B.120°
C.150°
D.135°
Chọn C.
Gọi người bơi là (1), dòng nước là (2)
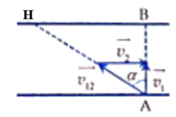
Để bơi sang sông với quãng đường ngắn nhất người đó phải bơi sao cho vận tốc v 12 ⇀ (vận tốc của người đối với nước) có hướng như hình vẽ để v 10 ⇀ (vận tốc của người đối với bờ sông) có phương vuông góc với bờ sông và thoả mãn:
v 10 ⇀ = v 20 ⇀ + v 12 ⇀
( v 20 ⇀ là vận tốc dòng chảy của nước)
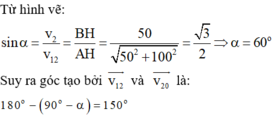
Đúng 0
Bình luận (0)
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng A. 600 B.1200 C.1500 D.1350
Đọc tiếp
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng
A. 600
B.1200
C.1500
D.1350
Đáp án B
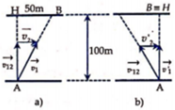
Gọi người là (1), dòng nước là (2)
Khi bơi theo hướng vuông góc với dòng chảy (hình a), khi đó người bơi đến điểm B, cách H một khoảng 50m
⇒ v 2 v 12 = 1 2
Để điểm B trùng với điểm H, hướng bơi ngoài đó (so với nước) có v 12 → phải như hình b
⇒ sin α = v 2 v 12 . Lưu ý : v 2 = v
Vậy sin α = 1 2 ⇒ α = 60 0
Nghĩa là người đó phải bơi theo hướng tạo với dòng chảy (tạo với v 2 → ) một góc bằng 1200
Đúng 0
Bình luận (0)
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng A.
60
°
B.
120
°
C.
150
°
D....
Đọc tiếp
Một người bơi từ điểm A của bờ sông bên này sang bờ bên kia của một con sông rộng 100m. Khi người đó bơi theo hướng vuông góc với dòng chảy thì điểm đến bờ bên kia (điểm B) cách vị trí đối diện với A (điểm H) một khoảng 50m. Để người đó sang bờ bên kia tại đúng vị trí đối diện với điểm A thì người đó phải bơi theo hướng tạo với hướng của dòng chảy một góc bằng
A. 60 °
B. 120 °
C. 150 °
D. 135 °
Chọn C.
Gọi người bơi là (1), dòng nước là (2)
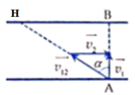
Để bơi sang sông với quãng đường ngắn nhất người đó phải bơi sao cho vận tốc v 12 → (vận tốc của người đối với nước) có hướng như hình vẽ để v 10 → (vận tốc của người đối với bờ sông) có phương vuông góc với bờ sông và thoả mãn:
v 10 → = v 12 → + v 20 →
( v 20 → là vận tốc dòng chảy của nước)
Từ hình vẽ:
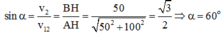
Suy ra góc tạo bởi v 12 → và v 20 → là:
![]()
Đúng 0
Bình luận (0)
Một ca nô đi ngang qua sông, xuất phát từ điểm A, mũi hướng vào một điểm B trên bờ sông bên kia. AB vuông góc với bờ sông. Nhưng do dòng nước chảy nên sau một thời gian t100s, ca nô đến một vị trí C ở bờ bên kia, cách B một đoạn BC 200 m. Nếu người lái giữ cho mũi ca nô luôn hướng theo phương chếch với bờ sông một góc 60 và mở máy như trước thì ca nô sẽ sang đến đúng điểm B. Hãy tìm: a. Vận tốc của dòng nước so với bờ sông. b. Vận tốc của ca nô so với dòng nước. c. Chiều rộng d của dòng sông. d....
Đọc tiếp
Một ca nô đi ngang qua sông, xuất phát từ điểm A, mũi hướng vào một điểm B trên bờ sông bên kia. AB vuông góc với bờ sông. Nhưng do dòng nước chảy nên sau một thời gian t=100s, ca nô đến một vị trí C ở bờ bên kia, cách B một đoạn BC =200 m. Nếu người lái giữ cho mũi ca nô luôn hướng theo phương chếch với bờ sông một góc 60 và mở máy như trước thì ca nô sẽ sang đến đúng điểm B. Hãy tìm: a. Vận tốc của dòng nước so với bờ sông. b. Vận tốc của ca nô so với dòng nước. c. Chiều rộng d của dòng sông. d. Thời gian để ca nô qua sông trong trường hợp ca nô cập bến B
Cho (1) là ca nô, (2) là nước, (3) là bờ sông.
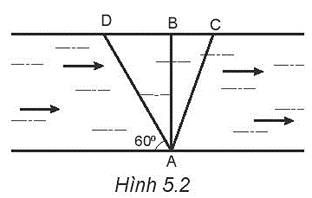
(a) Trong 100s, nước chảy đưa ca nô chếch từ vị trí B đến C, nên vận tốc của dòng nước so với bờ là: \(v_{23}=\dfrac{BC}{t}=\dfrac{200}{100}=2\left(m/s\right)\)
(b) Dựa vào hình vẽ, dễ thấy: \(\hat{ADB}=\alpha=60^o\).
Khi đi theo hướng \(AD:v_{12}=v_{12}';v_{23}=v_{23}'=2\left(m/s\right)\)
\(v_{23}'\) là vận tốc của dòng nước so với bờ sông, tức vecto này hướng theo hướng vector \(\overrightarrow{DB}\), \(v_{12}'\) là vận tốc của ca nô so với dòng nước, tức vecto này theo hướng vector \(\overrightarrow{AD}\).
Dựa vào hình vẽ và hệ thức lượng trong tam giác vuông: \(v_{12}'=\dfrac{v_{23}'}{cos\hat{ADB}}=\dfrac{2}{cos60^o}=4\left(m/s\right)\).
(c) Khi đi theo hướng \(AC\), vector \(\overrightarrow{v_{12}}\) hướng theo hướng vector \(\overrightarrow{AB}\)
\(\Rightarrow AB=v_{12}t=4\cdot100=400\left(m\right)\)
(d) Khi đi theo hướng \(AD\), vận tốc của thuyền so với bờ là \(v_{13}'=v_{12}'sin\hat{ADB}=4\cdot sin60^o=2\sqrt{3}\left(m/s\right)\)
Thời gian qua sông lần sau: \(t'=\dfrac{AB}{v_{13}'}=\dfrac{400}{2\sqrt{3}}\approx115,47\left(s\right)\)
Đúng 1
Bình luận (0)
Trên một khúc sông với hai bờ song song với nhau, một người lái đò dựđịnh chèo đò qua sông từ vị trí A ở bờ bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Người lái đò đã xuất phát từ A và lái đò theo phương vuông góc với bờ sông, do đó con đò bị dòng nước đẩy xiên và cập bến ở bờ bên kia tại vị trí C cách B một đoạn 45 m. Biết khúc sông rộng 270 m, hỏi dòng nước đã đẩy chiếc đò lệch một góc có số đo bằng bao nhiêu so với phương AB? (làm tròn kết quả đến phút).
Đọc tiếp
Trên một khúc sông với hai bờ song song với nhau, một người lái đò dự
định chèo đò qua sông từ vị trí A ở bờ bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Người lái đò đã xuất phát từ A và lái đò theo phương vuông góc với bờ sông, do đó con đò bị dòng nước đẩy xiên và cập bến ở bờ bên kia tại vị trí C cách B một đoạn 45 m. Biết khúc sông rộng 270 m, hỏi dòng nước đã đẩy chiếc đò lệch một góc có số đo bằng bao nhiêu so với phương AB? (làm tròn kết quả đến phút).
Câu 5: Một chiếc đò chèo ngang qua sông bị dòng nước đẩy chiếc đò lệch đi một góc xấp xỉ là 54o. Đoạn đường chiếc đò đi qua bến bờ bên kia khoảng 240 mét. Tính bề rộng của con sông (làm tròn đến mét)
Một dòng sông có chiều rộng là 60m nước chảy với vận tốc 1m/s so với bờ. Một người lái đò chèo một chiếc thuyền đi trên sông với vận tốc 3m/s.Khi đi từ bờ này theo phương vuông góc sang bờ đối diện (điểm dự định đến). Do nước chảy nên khi sang đến bờ kia, thuyền bị trôi về phía cuối dòng.Khoảng cách từ điểm dự định đến và điểm thuyền đến thực cách nhau là? A. m B. 20m C. 63m D. 18m
Đọc tiếp
Một dòng sông có chiều rộng là 60m nước chảy với vận tốc 1m/s so với bờ. Một người lái đò chèo một chiếc thuyền đi trên sông với vận tốc 3m/s.
Khi đi từ bờ này theo phương vuông góc sang bờ đối diện (điểm dự định đến). Do nước chảy nên khi sang đến bờ kia, thuyền bị trôi về phía cuối dòng.Khoảng cách từ điểm dự định đến và điểm thuyền đến thực cách nhau là?
A. m
B. 20m
C. 63m
D. 18m
Đáp án B.
Trong khoảng thời gian thuyền đi ngang từ A đến B ,
nước đi dọc từ B đến C nên ta có A B B C = v t n v n b = 3 ⇒ B C = A B 3 = 20 m
Đúng 0
Bình luận (0)
Một dòng sông có chiều rộng là 60m nước chảy với vận tốc 1m/s so với bờ. Một người lái đò chèo một chiếc thuyền đi trên sông với vận tốc 3m/s Khi đi từ bờ này theo phương vuông góc sang bờ đối diện (điểm dự định đến). Do nước chảy nên khi sang đến bờ kia, thuyền bị trôi về phía cuối dòng.Khoảng cách từ điểm dự định đến và điểm thuyền đến thực cách nhau là? A. 180 m B. 20 m C. 63 m D. 18 m
Đọc tiếp
Một dòng sông có chiều rộng là 60m nước chảy với vận tốc 1m/s so với bờ. Một người lái đò chèo một chiếc thuyền đi trên sông với vận tốc 3m/s
Khi đi từ bờ này theo phương vuông góc sang bờ đối diện (điểm dự định đến). Do nước chảy nên khi sang đến bờ kia, thuyền bị trôi về phía cuối dòng.Khoảng cách từ điểm dự định đến và điểm thuyền đến thực cách nhau là?
A. 180 m
B. 20 m
C. 63 m
D. 18 m
Đáp án B.
Trong khoảng thời gian thuyền đi ngang từ A đến B ,
nước đi dọc từ B đến C nên ta có
A B B C = v t n v n b = 3 ⇒ B C = A B 3 = 20 m
Đúng 0
Bình luận (0)









