Trên bảng có các số \(\frac{1}{96};\frac{2}{96};...;\frac{96}{96}.\)Mỗi một lần thực hiện, cho phép xóa đi hai số a,b bất kỳ trên bảng và thay bằng a+b-2ab. Hỏi sau 95 lần thực hiện phép xóa, số còn lại trên bảng có giá trị bằng bao nhiêu?

Những câu hỏi liên quan
Câu 2 (0,5đ): Cho bảng thống kê sau :Giá trị (x)Tần số(n)Các tích 4…………… 5 10 2X 67………..... 10110 N........Tổng : 96 a) Tìm các số còn thiếu trong bảng trên và điền kết quả vào bảng.
Đọc tiếp
Câu 2 (0,5đ):
Cho bảng thống kê sau :
Giá trị (x) | Tần số(n) | Các tích |
|
|
|
4 | ……… | …… |
|
|
|
5 |
| 10 |
|
|
|
2 | X = 6 | ||||
7 | ………. | .... |
|
|
|
10 | 1 | 10 |
|
|
|
| N=........ | Tổng : 96 |
|
|
|
a) ![]()
Tìm các số còn thiếu trong bảng trên và điền kết quả vào bảng.
Cho bảng 2 x n. Trên bảng điền 2n số thực dương sao cho tổng của các số trên 1 cột bằng 1. Chứng minh : Có thể chọn trên mỗi cột 1 số sao cho tổng các số đã chọn trên từng hàng nhỏ hơn bằng \(\frac{n+1}{4}\)
Viết trên bảng các số \(-\frac{1}{2019};-\frac{2}{2019};-\frac{3}{2019};...;-\frac{2019}{2019}\). Mỗi lần ta xóa đi 2 số a,b rồi thay vào đó số a+3ab+b. Sau 2018 lần thực hiện như vậy, trên bảng chỉ còn lạ 1 số. Hỏi đó là số có giá trụ bằng bao nhiều? Vì sao?
Dễ thấy trong 2019 số trên có 1 số là \(-\dfrac{673}{2019}=-\dfrac{1}{3}\)
Khi xoá 1 số bất kì x khác -1/3 thuộc dãy số đó với số -1/3 ta được số mới là
\(x+3x.\dfrac{-1}{3}+\left(-\dfrac{1}{3}\right)=-\dfrac{1}{3}\)
Như vậy, sau khi xoá đủ 2018 lần thì số còn lại vẫn là -1/3
Đúng 3
Bình luận (0)
a, Cho x , y , z là các số thực thỏa mãn left(x-yright)left(x-zright)1;yne z. Chứng minh : frac{1}{left(x-yright)^2}+frac{1}{left(y-zright)^2}+frac{1}{z-x}^2ge4.b, Trên bảng ban đầu ghi số 2 và số 4 . Ta thực hiện cách viết thêm các số lên bảng như sau : nếu trên bảng đã có 2 số , a,b ; ane b, ta viết thêm lên bảng số có giá trị là a + b + ab . Hỏi với cách thực hiện như vậy , trên bảng có thể suất hiện số 2016 được hay không ? Giải thích .
Đọc tiếp
a, Cho x , y , z là các số thực thỏa mãn \(\left(x-y\right)\left(x-z\right)=1;y\ne z\). Chứng minh :
\(\frac{1}{\left(x-y\right)^2}+\frac{1}{\left(y-z\right)^2}+\frac{1}{z-x}^2\ge4.\)
b, Trên bảng ban đầu ghi số 2 và số 4 . Ta thực hiện cách viết thêm các số lên bảng như sau : nếu trên bảng đã có 2 số , a,b ; \(a\ne b\), ta viết thêm lên bảng số có giá trị là a + b + ab . Hỏi với cách thực hiện như vậy , trên bảng có thể suất hiện số 2016 được hay không ? Giải thích .
Trên bảng viết các số \(\frac{1}{2018};\frac{2}{2018};......;\frac{2017}{2018};\frac{2018}{2018}\)
Mỗi lần biến đổi bằng cách xóa đi hai số a,b bất kì và thay bằng số a+b-2ab.Hỏi sau 2017 lần thực hiện phép biến đổi thì trên bảng còn lại số nào?
Cho hàm số fleft( x right) frac{1}{{x - 1}} có đồ thị như Hình 4.x 1,11,011,0011,0001y f(x)10100?? Từ đồ thị và bảng trên, có nhận xét gì về giá trị fleft( x right) khi x dần tới 1 phía bên phải?b) Tìm các giá trị còn thiếu trong bảng sau:x0,90,990,9990,9999y f(x)– 10– 100?? Từ đồ thị và bảng trên, có nhận xét gì về giá trị fleft( x right) khi x dần tới 1 phía bên trái?
Đọc tiếp
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
x
1,1
1,01
1,001
1,0001
y = f(x)
10
100
?
?
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
x | 0,9 | 0,99 | 0,999 | 0,9999 |
y = f(x) | – 10 | – 100 | ? | ? |
Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
a)

Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)
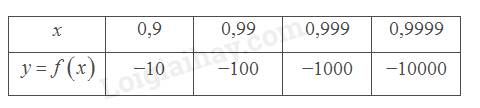
Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.
Đúng 0
Bình luận (0)
Trên bảng có các số 1/2015,2/2015,3/2015,...,2014/2015.
Mỗi lần ta xóa 2 số bất kì a, b có trên bảng rồi viết số a+b-5ab. Sau 2013 lần làm theo công thức trên, số nào còn lại trên bảng?
Trích đề thi HSG lớp 8 huyện Nho Quan 2020 - 2021Câu 5( 2,0 điểm )1. Cho tam giác ABC vuông tại A có độ dài cạnh huyền là a và độ dài đường cao xuất phát từ đỉnh A kẻ xuống cạnh đối diện BC là h.Tìm GTNN của biểu thức Q30frac{a}{h}+4frac{h}{a}+19752. Cho n là một số nguyên dương lẻ. Ta viết các số 1, 2, 3, ... ,2n lên bảng. Ta thực hiện việc xóa hai số bất kì trên bảng ( ví dụ a,b ) và thay vào đó số | a - b |. Việc đó được thực hiện đến khi trên bảng còn đúng một số. Hỏi với cách làm như trên t...
Đọc tiếp
Trích đề thi HSG lớp 8 huyện Nho Quan 2020 - 2021
Câu 5( 2,0 điểm )
1. Cho tam giác ABC vuông tại A có độ dài cạnh huyền là a và độ dài đường cao xuất phát từ đỉnh A kẻ xuống cạnh đối diện BC là h.
Tìm GTNN của biểu thức \(Q=30\frac{a}{h}+4\frac{h}{a}+1975\)
2. Cho n là một số nguyên dương lẻ. Ta viết các số 1, 2, 3, ... ,2n lên bảng. Ta thực hiện việc xóa hai số bất kì trên bảng ( ví dụ a,b ) và thay vào đó số | a - b |. Việc đó được thực hiện đến khi trên bảng còn đúng một số. Hỏi với cách làm như trên thì số 2022 có mặt trên bảng hay không ?
vu ngc hieu hoc lop may roi day ?
Xem thêm câu trả lời
Cho các biểu thức sau: 25 + frac{35}{365}+ frac{40}{365}+ 25 + frac{35+40}{365x2}(1), 96 x 1+ 96 x 2 + frac{96+96}{1+2}x frac{96+1+2}{96.2+1+2}(2).Nếu kết quả của biểu thức (1) là frac{x}{73}thì kết quả của biểu thức (2) là frac{y}{72-5}. Biết y - x 17167, x + y 24497. Tìm tử số của hai biểu thức đó. Biết rằng biểu thức (1) có tử số đến hàng nghìn, biểu thức (2) có tử số đến hàng chục nghìn và hai phân số của (1) là frac{35}{365}frac{40}{365}, hai phân số của (2) là frac{96+96}{1+2}frac{96+1+2...
Đọc tiếp
Cho các biểu thức sau: 25 + \(\frac{35}{365}\)+ \(\frac{40}{365}\)+ 25 + \(\frac{35+40}{365x2}\)(1), 96 x 1+ 96 x 2 + \(\frac{96+96}{1+2}\)x \(\frac{96+1+2}{96.2+1+2}\)(2).
Nếu kết quả của biểu thức (1) là \(\frac{x}{73}\)thì kết quả của biểu thức (2) là \(\frac{y}{72-5}\). Biết y - x = 17167, x + y = 24497. Tìm tử số của hai biểu thức đó. Biết rằng biểu thức (1) có tử số đến hàng nghìn, biểu thức (2) có tử số đến hàng chục nghìn và hai phân số của (1) là \(\frac{35}{365}<\frac{40}{365}\), hai phân số của (2) là \(\frac{96+96}{1+2}>\frac{96+1+2}{96.2+1+2}\).
giải theo lớp 8 thì hệ phương trình đã cho y=20832
Đúng 0
Bình luận (0)

















