So sánh độ dài các cạnh của tứ giác ABCD ở hình 56.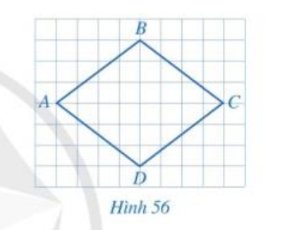

Những câu hỏi liên quan
Cho hình tứ giác ABCD . Kẻ đường chéo BD . Từ C vẽ một đường thẳng song song với BD cắt cạnh AD kéo dài ở điểm E . Nối B với E . Hãy so sánh diện tích hình tam giác ABE với diện tích hình tứ giác ABCD .
Tứ giác ABCD có ∠ B = ∠ D = 90 °
So sánh độ dài AC và BD. Nếu AC = BD thì tứ giác ABCD là hình gì?
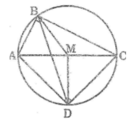
Trong đường tròn tâm M ta có BD là dây cung không đi qua tâm, AC là đường kính nên: BD < AC
AC = BD khi và chỉ khi BD là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.
Đúng 0
Bình luận (0)
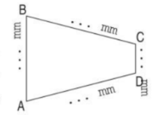
a) Đo độ dài các cạnh của hình tứ giác ABCD rồi viết số thích hợp vào chỗ chấm.
b) Tính chu vi hình tứ giác ABCD.
Phương pháp giải:
- Dùng thước kẻ đo chiều dài của mỗi cạnh rồi điền vào chỗ trống.
- Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Lời giải chi tiết:
a) Độ dài các cạnh của hình tứ giác đo được là:
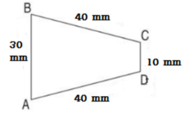
b) Chu vi hình tứ giác ABCD là :
40 + 10 + 40 + 30 = 120 (mm)
Đáp số: 120mm.
Đúng 0
Bình luận (0)
a) Đo độ dài các cạnh của hình tứ giác ABCD rồi viết số thích hợp vào chỗ chấm.
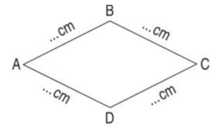
b) Tính chu vi hình tứ giác ABCD.
Phương pháp giải:
- Dùng thước kẻ đo độ dài các cạnh của hình tứ giác rồi điền vào chỗ trống.
- Chu vi hình tứ giác bằng tổng độ dài bốn cạnh của hình đó.
Lời giải chi tiết:
a)
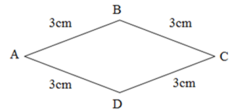
b)
Chu vi hình tứ giác ABCD là :
3 + 3 + 3 + 3 = 12 (cm)
Đáp số: 12 cm.
Đúng 0
Bình luận (0)
So sánh độ dài cạnh AB và đường chéo BD của tứ giác ABCD biết chi vi tam giác ABD bé hơn hoạc bằng chu vi tam giác ACD
Quan sát hình bình hành ở hình 4.12a.
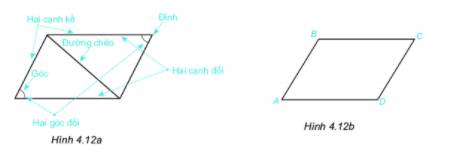
1. Dùng thước thẳng đo và so sánh độ dài các cạnh đổi của hình bình hành ABCD (1.4.12b).
2. Các góc đối của hình bình hành ABCD có bằng nhau không?
3. Các cạnh đối của hình bình hành ABCD có song song với nhau không?
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
Đúng 1
Bình luận (0)
Bài 4: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB,
BC, CD, DA.
a) CMR: Tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ và tổng hai đường chéo của tứ giác ABCD.
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) CMR: Tứ giác MNPQ là hình bình hành
b) So sánh chu vi tứ giác MNPQ và tổng hai đường chéo của tứ giác ABCD.
Xem chi tiết
cho hình tứ giác ABCD . Gọi M,N,P,Q lần lượt là các điểm chính giữa của các cạnh AB , BC , CD , DA . hãy so sánh S của tứ giác MNPQ và diện tích ABCD
KO CÓ HÌNH NHA
So sánh độ dài cạnh AB và đường chéo AC của tứ giác ABCD biết rằng chu vi tam giác ABD nhỏ hơn hoặc bằng chu vi tam giác ACD
Bạn ơi câu đàu tiên phải là "của tứ giác ABCD" nhé, mình đánh máy nhầm.
Mà bạn là VIP bias T.O.P đúng hơm,y chang mình. Kết bạn nhoa~
Đúng 0
Bình luận (0)
Gọi O là giao điểm 2 đường chéo AC và BD cảu tứ giác ABCD.
Xét tam giác AOB, theo bất đẳng thúc tam giác, ta có: AB<OA+OB
Xét tam giác COD, theo bất đẳng thức tam giác, ta có: CD<OC+OD
Suy ra: AB+CD<OA+OB+OC+OD
hay AB+CD<AC+BD (1)
Ta lại có: AB+BD+AD=<AC+CD+AD
\(\Rightarrow\) AB+BD=<AC+CD
\(\Rightarrow\) AB-CD=<AC-BD (2)
Từ (1) và (2), suy ra: 2AB<2AC (cộng vế theo vế)
\(\Rightarrow\) AB<AC (đpcm)
Đảm bảo chính xác 100%
Độ tin cậy không cần bàn cãi.
Đúng 1
Bình luận (0)














