Cho: a,b,c,d,e khác 0;
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{e}\)
CM:\(\frac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}=\frac{a}{c}\)
Nếu sai đề thì bảo mình tiếng nhé ! ''^_^''
cho ab =bc=cd=de=ea .chứng minh a=b=c=d=e.(a,b,c,d,e là số nguyên và khác 0)
cho các số thực a b c d khác 0 thoỏa mãn a/b=b/c=c/d=d/e
Cho 5 chữ số a ; b ; c ; d ; e với a khác b khác c khác d khác e khác 0 . Hỏi thành lập được bao nhiêu số có mặt cả 5 chữ số ở trên ? Tìm cách tính tổng của tất cả các số đó.
Help me!!!
Cho a phần b = c phần d. Chứng minh:
a) a phần b = a+c phần b+d .
b) a-b phần b = c-d phần d .
c) a+b phần b = c+d phần d.
d) a phần a+b = c phần c+d ( a+b khác 0 và c+d khác 0 ).
e) a-b phần a+b = c-d phần c+d.
search mạn bn à. Mà bài này dễ CM mà công thức trong sách giáo khoa lớp 7 hả.......
Cho 7 chữ số khác 0 là a, b, c, d, e, f, g. Biết \(a^b=b^c=c^d=d^e=e^f=f^g=g^a\). Chứng minh rằng a=b=c=d=e=f=g
•Ghi lời giải rõ ràng giúp mình.
if a<b,bcz of a^b=b^c so b>c c<d d>e e<f f>g g<a bcz of g<a and a<b so g<b (not possible)
Same with a>b ,so a=b.
Do again multiple time ,we get a=b=c=d=e=f so bcs f^g=g^a,so f^g=g^f so g=f.
So totally ,we get a=b=c=d=e=f=g.
Cho số hực dương a,b,c,d, e khác 0 thỏa mãn\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\)
Chứng minh rằng\(\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}\)=\(\dfrac{a}{e}\)
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}=k\Rightarrow a=bk;b=ck;c=dk;d=ek\)
\(\Rightarrow a=bk=ck^2=dk^3=ek^4;b=ek^3\)
\(\Rightarrow\dfrac{a}{e}=\dfrac{ek^4}{e}=k^4\left(1\right)\)
Ta có \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\Rightarrow\dfrac{a^4}{b^4}=\dfrac{b^4}{c^4}=\dfrac{c^4}{d^4}=\dfrac{d^4}{e^4}=\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}\left(2\right)\)
Lại có \(\dfrac{a^4}{b^4}=\left(\dfrac{a}{b}\right)^4=\left(\dfrac{ek^4}{ek^3}\right)^4=k^4\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\RightarrowĐpcm\)
Cho hàm số đa thức bậc ba y = f (x) có đồ thị đi qua các điểm A(2;4), B(3;9), C(4;16). Các đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các điểm D, E, F (D khác A và B, E khác A và C, F khác B và C). Biết rằng tổng các hoành độ của D, E, F bằng 24. Tính f(0)
A. π 4
B. 0
C. 24 5
D. 2
Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
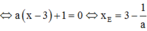
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó 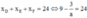
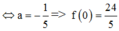
cho bảy số tự nhiên khác 0 là a,b,c,d,e,g,h
thõa mãn:ab=bc=cd=de=eg=gh=ha
chứng minh rằng:a=b=c=d=e=g=h
Câu 1 :Cho tỉ lệ thức a/b=c/d với b,c,d khác 0và c khác -d
Cmr: a+b/b=c+d/d
Câu 2: cho tỉ lệ thức a/b=c/d với b,c,d khác 0 và a khác -b,c khác -d.
Cmr: a/a+b=c/c+d
Câu 3: cho a+b/a-b=c+d/c-d(a,b,c,d khác 0 và a khác b, c khác âm dương c)
Cmr a/b=c/d
Câu 4: cho tỉ lệ thức a/b=c/d với a,b,c,d khác 0
Cmr ac/bd=a^2+c^2 /b^2+d^2
Câu 5: cho tỉ lệ thức a/b=c/d với a,b,c,d khác 0 và c khác d
Cmr: (a-b)^2/(c-d)^2=ab/cd
Câu 6: cho tỉ lệ thức a/b=c/d với a,b,c,d khác 0 và khác-d
Cmr: (a+b)^2014/(c+d)^2014=a^2014+b^2014/c^1014+d^2014
Câu 7:cho a/c=c/d với a,b,c khác 0
Cmr a/b=a^2+c^2/b^2+d^2
Câu 8: cho a/c=c/d với a,b,c khác 0
Cmr b-a/a=b^2-a^2/a^2+c^2
Câu 9:cho tỉ lệ thức a/b=c/d với a,b,c,d khác 0 và a khác âm dương 5/3b; khác âm dương 5/3d khác 0
Cmr: các tỉ lệ thức sau: 3a+5b/3a-5b=3c+5d/3c-5d
Câu 10: cho tỉ lệ thức a/b=c/d với a,b,c,d khác 0
Cmr: 7a^2+5ac/7b^2-5ac=7a^2+5bd/7b^2-5bd
Câu 1
Ta có : \(\frac{a}{b}=\frac{c}{d}=>\left(\frac{a}{b}+1\right)=\left(\frac{c}{d}+1\right)\left(=\right)\frac{a+b}{b}=\frac{c+d}{d}\)
=> ĐPCM
Câu 2
Ta có \(\frac{a}{b}=\frac{c}{d}=>\frac{b}{a}=\frac{d}{c}=>\left(\frac{b}{a}+1\right)=\left(\frac{d}{c}+1\right)\left(=\right)\frac{b+a}{a}=\frac{d+c}{c}=>\frac{a}{b+a}=\frac{c}{d+c}\)
=> ĐPCM
Câu 3
Câu 3
Ta có \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)(=) (a+b).(c-d)=(a-b).(c+d)(=)ac-ad+bc-bd=ac+ad-bc-bd(=)-ad+bc=ad-bc(=) bc+bc=ad+ad(=)2bc=2ad(=)bc=ad=> \(\frac{a}{b}=\frac{c}{d}\)
=> ĐPCM
Câu 4
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(=>\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Ta có \(\frac{ac}{bd}=\frac{bk.dk}{bd}=k^2\left(1\right)\)
Lại có \(\frac{a^2+c^2}{b^2+d^2}=\frac{b^2k^2+c^2k^2}{b^2+d^2}=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ (1) và (2) => ĐPCM
Mày là thằng anh tuấn lớp 7c trường THCS yên lập đúng ko