Đánh giá được mức đơn giản của thuật toán, từ đó tìm ra được cách giải nhanh nhất.

Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.­­­­­­­mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

Thuật toán tìm kiếm tuần tự: Duyệt lần lượt các phần tử của dãy để tìm phần tử có giá trị bằng K. Nếu tìm thấy, trả về chỉ số của phản tử bằng K; Ngược lại, thông báo không tìm thây và trả về giá trị -1. Thuật toán có thê duyệt từ đâu dãy hoặc từ cuối dãy.

Số lần so sánh giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần so sánh giữa các phần tử là cố định, không phụ thuộc vào dữ liệu đầu vào. Cụ thể, số lần so sánh trong thuật toán sắp xếp chọn là \(\dfrac{n\left(n-1\right)}{2}\), với n là số phần tử trong mảng hoặc danh sách.

Số lần hoán đổi giữa các phần tử: Trong thuật toán sắp xếp chọn, số lần hoán đổi giữa các phần tử có thể đạt đến tối đa n-1 lần, với n là số phần tử trong mảng hoặc danh sách.

Vậy độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n²), hay \(\dfrac{n\left(n-1\right)}{2}\) lần so sánh và tối đa n-1 lần hoán đổi giữa các phần tử.

Tham khảo:

QT1. Quy tắc cộng: O(f(n)+g(n))=O(max(f(n),g(n)))

QT2. Quy tắc nhân:

- Với hằng sô: O(C.f(n))=O(f(n))

- Với hàm số: O(f(n).g(n))=O(f(n)).O(g(n))

1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.

2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.

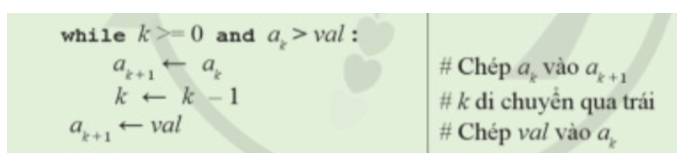
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:

Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.

Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1

Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.

Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.

tính E(300)=300/log2(300), E(90000)=90000/log2(90000)

Vì độ hiệu quả tỉ lệ thuận với thời gian thực hiện

nên ta có tỉ số 0,02/E(300)=x/E(90000) (x là giá trị cần tìm).

Từ đó tính được x=3