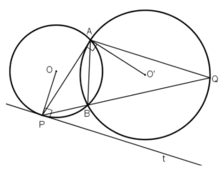
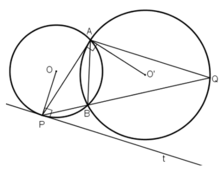
Cho hai đường tròn (O;R) và (O';R') cắt nhau tại A và B. (O và O' nằm ở hai nửa mặt phẳng bờ AB.) Một đường thẳng qua A cắt đường tròn (O) và (O') tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE song song với KD (E thuộc BD).
a/ Chứng minh tam giác BOO' đồng dạng với tam giác BCD.
b/ Chứng minh tứ giác BCKD là tứ giác nội tiếp
c/ Chứng minh AE là tiếp tuyến của đường tròn (O;R)
d/ Tìm vị trí của CD để diện tích tam giác BCD lớn nhất













 ΔPBO
ΔPBO

 ΔPBO
ΔPBO