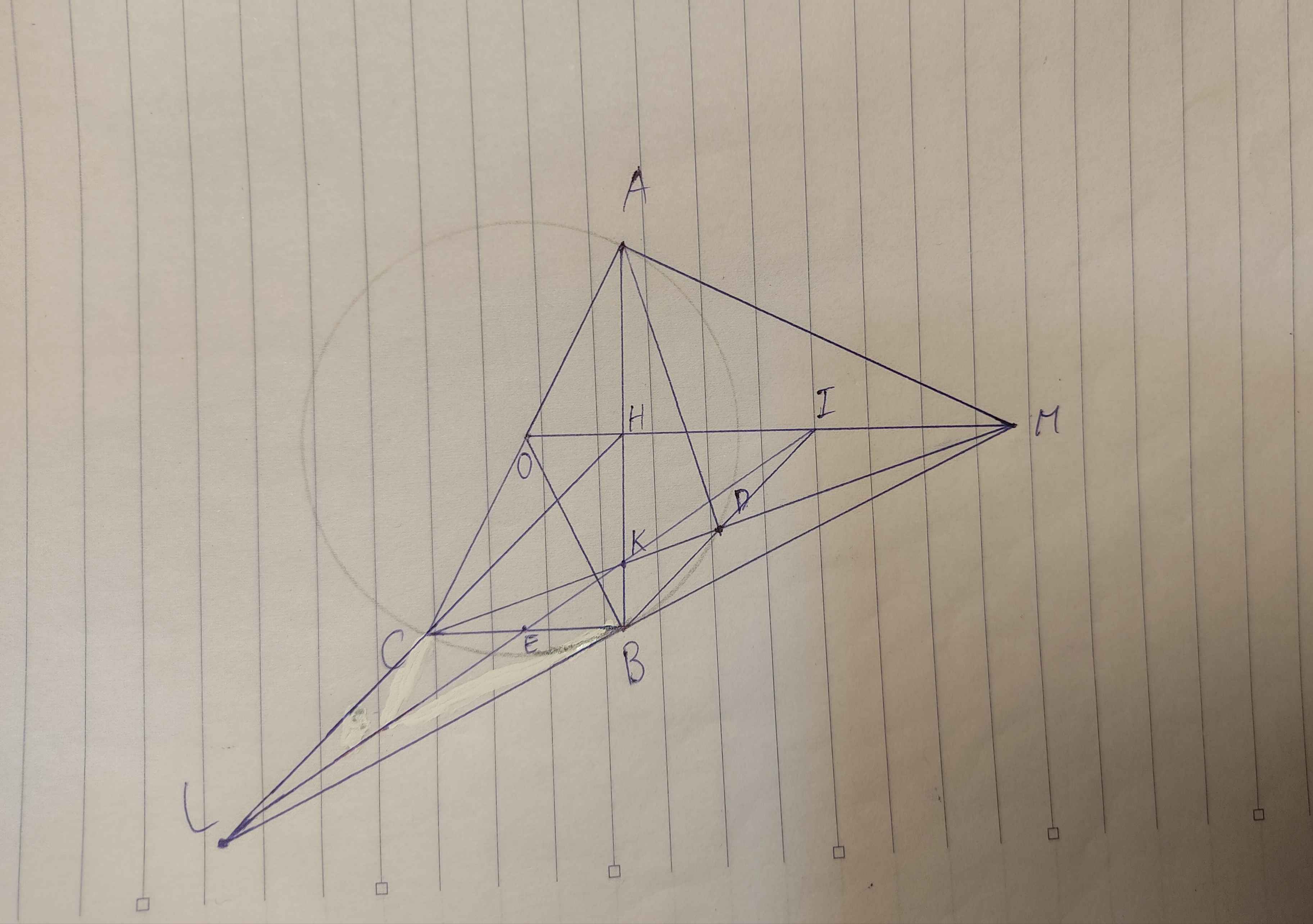
Các bạn giúp mình làm ý d với ạ! Mình xin cảm ơn các bạn
Từ điểm M nằm ngoài đường tròn vẽ tiếp tuyến MA tới đường tròn (O; R), ( A là tiếp điểm). Gọi E là trung điểm đoạn AM và hai điểm I, H lần lượt là hình chiếu của E và A trên đường thẳng OM. Qua M vẽ cát tuyến MBC tới đường tròn (O) sao cho MB < MC và tia MC nằm giữa hai tia MA, MO.
a) Chứng minh các hệ thức: MA2 = MB.MC; MA2 = MH.MO.
b) Chứng minh ∆MBH đồng dạng ∆MOC. Từ đó chứng minh tứ giác BCOH nội tiếp đường tròn.
c) Chứng minh . Vẽ tiếp tuyến IK tới đường tròn (O) với K là tiếp điểm. và ∆MKH vuông tại K.
d) Giả sử BC = 3BM và D là trung điểm đoạn MC. Chứng minh: MC tiếp xúc với đường tròn ngoại tiếp ∆ODH