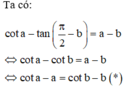Cho các số thực a, b, c thỏa mãn điều kiện: a>0; \(bc=2a^2\)và a+b+c=abc. Chứng minh rằng \(a\ge\sqrt{\frac{1+2\sqrt{2}}{2}}\)

Những câu hỏi liên quan
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Đúng 1
Bình luận (0)
Cho các số thực a, b, c thỏa mãn điều kiện : (0 < c < b< a<=3); (2ab <= 2a+3b); (3abc <= ab+3bc+2ca.)
Chứng minh rằng a³ +b³ + c³<= 36.
Cho a;b;c là ba số thực dương,
a
1
và thỏa mãn
log
2
a
b
c
+
log
a
b
3
c
3
+
b
c...
Đọc tiếp
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Đúng 0
Bình luận (0)
cho a,b,c là ba số thực khác 0 thỏa mãn điều kiện a+b-c/c = b+c-a/a = c+a-b/b
Cho a, b là các số thực thuộc khoảng
0
;
π
2
thỏa mãn điều kiện cota - tan
π
2
-
b
a-b. Tính giá trị biểu thức
P
3
a
+
7
b
a...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 thỏa mãn điều kiện cota - tan π 2 - b = a-b. Tính giá trị biểu thức P = 3 a + 7 b a + b
A. P = 5
B. P = 2
C. P = 4
D. P = 6
Cho a,b,c là các số thực khác 0 thỏa mãn điều kiện:
\(\hept{\begin{cases}\text{a^2( b + c ) + b^2( c + a ) + c^2( a + b ) + 2abc = 0}\\a^{2015}+b^{2015}+c^{2015}=1\end{cases}}\)
Cho a, b là các số thực thuộc khoảng
0
;
π
2
và thỏa mãn điều kiện
c
o
t
a
-
tan
π
2
-
b
a
-
b
.Tính giá trị của biểu thức
P
3...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 và thỏa mãn điều kiện c o t a - tan π 2 - b = a - b .Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Tìm các số thực x thỏa mãn điều kiện
1
2
a
x
+
a
-
x
1
a
0
,
a
≠
1
A. 3 B. 2 C. 1 D...
Đọc tiếp
Tìm các số thực x thỏa mãn điều kiện 1 2 a x + a - x = 1 a > 0 , a ≠ 1
A. 3
B. 2
C. 1
D. 0
Tìm các số thực x thỏa mãn điều kiện
1
2
(
a
x
+
a
-
x
)
1
a
0
,
a
≠
1
A. 3 B. 2 C. 1 D. 0
Đọc tiếp
Tìm các số thực x thỏa mãn điều kiện 1 2 ( a x + a - x ) = 1 a > 0 , a ≠ 1
A. 3
B. 2
C. 1
D. 0
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện
log
a
x
log
b
x
0
log
c
x
. Mệnh đề nào sau đây đúng ? A. c a b B. b a c C. c b a D. a b c
Đọc tiếp
Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện log a x > log b x > 0 > log c x . Mệnh đề nào sau đây đúng ?
A. c > a > b
B. b > a > c
C. c > b > a
D. a > b > c
Đáp án B
Ta có:
log a x > log b x > 0 > log c x ⇔ 1 log x a > 1 log x b > 0 log x c < 0 ⇔ log x b > log x c > 0 c < 1 ⇔ b > a > 1 > c .
Đúng 0
Bình luận (0)