Giúp mk vs , cảm ơn mn nhìu
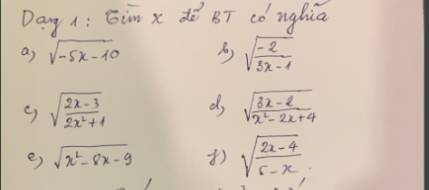
1 TAM GIÁC CÓ MN// BC. TÍNH MN NẾU BC LÀ 36CM
GIÚP MK VS NHÉ. MK CẢM ƠN NHÌU
MN là đường trung bình đúng không hay chỉ đơn thuần là song song thôi
Vẹ mik vs mn ơi mk cảm ơn nhìu
Câu 5:
Q=m.c.(t-t1)= 0,5. 4200.(80-20)=126000(J)
Câu 6:
Q(cung cấp)= m1.c1(t-t1)+m2.c2.(t-t2)= 0,5.880.(100-25)+ 2.4200.(100-25)=663000(J)
kb vs mk nha mn
cảm ơn mn nhìu ^-^
mình kb với bạn nhưng bữa sau bạn đừng đưa ra câu hỏi linh tinh nha.
Kb vs mk nha mn ^-^
cảm ơn mn nhìu lw
-.-
ở chọn nơi chơi chọn bạn
hãy kb và tk cho mik nếu bạn thấy mik xứng đáng
ukm
Nhwung lần sau cậu ko nên ra nhưng câu hỏi này

Mn giúp e vs ạ.E cảm ơn mn nhìu ạ
 giúp mình vs nha cảm ơn mn nhìu
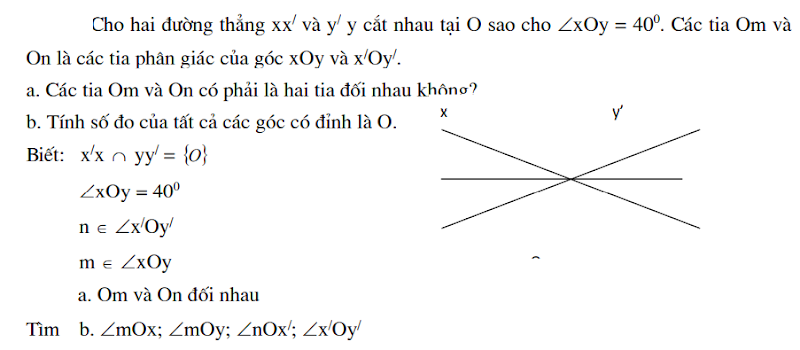
giúp mình vs nha cảm ơn mn nhìu
Nhờ mn giúp em vs ạ. Cảm ơn nhìu.
Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)
Kb vs mk ik mn
Cảm ơn mn nhìu lw
^-^
Kb vs mk nha mn
Cảm ơn mn nhìu nha
^-^