cho hình vuông abcd có cạnh bằng 12cm. Trên BC lấy M sao cho BM = 2/3 BC.
a) Tính S ABCD và S CAM.
b) Lấy điểm K là trung điểm của AM. Tính S ABK.
Cho hình chữ nhật ABCD có s là 48 Xăng-ti-mét vuông .Trên cạnh CD lấy điểm E sao cho ec=1/2ed .trên cạnh bc lấy điểm M sao cho BM =2/5 bc
A/tính s tam giác Amb
B/tính tỉ số giữa hai tam giác ABM VÀ CEM
C/tính diện tích tam giác AEM
a)Từ hình vẽ ta có diện tích tam giác ABC bằng diện tích tam giác ADC bằng diện tích tam giác BDC và bằng 1212 diện tích hình chữ nhật ABCD và bằng:
48:2=24 (cm2 )
Vì BM == MC nên diện tích tam giác ABM bằng 12 diện tích tam giác ABC
Diện tích tam giác ABM là:
24:2=12 (cm2 )
Vì DE == EC nên diện tích tam giác BEC bằng 12 diện tích tam giác BCD
Diện tích tam giác BEC là:
24:2=12 (cm2 )
Vì BM == MC nên diện tích tam giác EMC bằng 12 diện tích tam giác EBC
Diện tích tam giác CEM là:
12:2=6 (cm2 )
Tỉ số giữa diện tích tam giác ABM và CEM là:
12:6=2
Vậy diện tích tam giác ABM gấp đôi diện tích tam giác CEM
c) Vì DE == EC nên diện tích tam giác ADE bằng 12 diện tích tam giác ACD
Diện tích tam giác ADE là:
24:2=12 (cm2 )
Diện tích tam giác AEM là:
48−12−12−6=18 (cm2)
Đáp số: 18cm2
Từ hình vẽ ta có diện tích tam giác ABC bằng diện tích tam giác ADC bằng diện tích tam giác BDC và bằng 1/2 diện tích hình chữ nhật ABCD và bằng:
48:2=24 (cm2)
Vì BM = MC nên diện tích tam giác ABM bằng 1/2 diện tích tam giác ABC
Diện tích tam giác ABM là:
24:2=12 (cm2cm2 )
b) Vì DE = EC nên diện tích tam giác BEC bằng 1/2 diện tích tam giác BCD
Diện tích tam giác BEC là:
24:2=12 (cm2)
Vì BM = MC nên diện tích tam giác EMC bằng 1/2 diện tích tam giác EBC
Diện tích tam giác CEM là:
12:2=6 (cm2)
Tỉ số giữa diện tích tam giác ABM và CEM là:
12:6=2
Vậy diện tích tam giác ABM gấp đôi diện tích tam giác CEM
c) Vì DE == EC nên diện tích tam giác ADE bằng 1/2 diện tích tam giác ACD
Diện tích tam giác ADE là:
24:2=12 (cm2 )
Diện tích tam giác AEM là:
48−12−12−6=18 (cm2 )
Đáp số: 18cm2
mình làm lại nha sory
Cho hình vuông ABCD cạnh bằng 1. Trên cạnh AB lấy điểm M sao cho BM = 1, trên cạnh CD lấy điểm N sao cho DN = 1 và P là trung điểm BC. Tính cosMNP?
![]()
![]()
![]()
![]()
Cho hình vuông ABCD. Trên BC lấy điểm M sao cho BM=2/3 BC.
a) Tính diện tích tam giác ABM. Nếu độ dài cạnh hình vuông Abcd là 12cm
b) Kéo dài AM cắt cạnh DC kéo dài tại K. So sánh CK và DK
a, S ABM=48 cm 2
b,CK<DK( vì CK+DC=DK)
Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho BM = MN = NC = 1/3 BC. Tính diện tích của tứ giác ABMD theo S
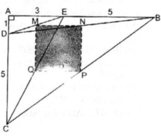
△ DMC có CM = 2/3BC
Hình bình hành ABCD và ΔDMC có chung đường cao kẻ từ đỉnh D đến BC.
Gọi độ dài đường cao là h, BC = a
Ta có diện tích hình bình hành ABCD là S = a h
S D M C = 1/2 h. 2/3 a = 1/3 ah = 1/3 S
S A B M D = S A B C D - S D M C = s - 1/3 S = 2/3 S
Cho hình vuông abcd trên BC lấy M sao cho BM bằng 2/3 BC a Tính diện tích ABM biết cạnh của hình vuông là 12 cm kéo dài AM cắt cạnh B C tại K. So sánh b c và c k (Làm cách lớp 5)
a)Độ dài đoạn thẳng BM là:
12 * 2/3 = 8 ( cm )
Diện tích hình tam giác ABM là:
12 * 8 / 2 = 48 ( cm2)
b) thấy sai sai ở đâu đó kìa
Đề bài nhầm vi M thuộc BC nên AM kéo dài phải cắt CD tại K mới đúng
Xét tam giác ABC và tam giác ABM có chung đường cao hạ từ A xuống AB ( chính là AB) nên
\(\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{2}{3}\Rightarrow S_{ABM}=\frac{2xS_{ABC}}{3}=\frac{2xABxAC}{2x3}=\frac{12x12}{3}=48cm^2\)
Xét tam giác ABC và tam giác ABK có đường cao hạ từ C xuống AB bằng đường cao hạ từ K xuống AB nên
\(\frac{S_{ABC}}{S_{ABK}}=\frac{AB}{AB}=1\Rightarrow S_{ABK}=S_{ABC}=\frac{ABxAC}{2}=\frac{12x12}{2}=72cm^2\)
\(S_{BKM}=S_{ABK}-S_{ABM}=72-48=24cm^2\)
Xét tam giác ABM và tam giác BKM có chung BM nên
S(BKM) / S(ABM) = đường cao hạ từ K xuống BC / đường cao hạ từ A xuống BC = 24/48=1/2
\(S_{ACM}=S_{ABC}-S_{ABM}=72-48=24cm^2\)
Xét tam giác ACM và tam giác CKM có chung đáy CM nên
S(CKM) / S(ACM) = đường cao hạ từ K xuống BC / đường cao hạ từ A xuống BC =1/2 => S(CKM) = S(ACM)/2=24/2=12 cm2
Xét tam giác BCD và tam giác MCD có cung đường cao hạ từ D xuống BC (chính là CD) nên
\(\frac{S_{MCD}}{S_{BCD}}=\frac{MC}{BC}=\frac{1}{3}\Rightarrow S_{MCD}=\frac{S_{BCD}}{3}=\frac{BCxCB}{2x3}=\frac{12x12}{6}=24cm^2\)
Xét tam giác MCD và tam giác CKM có chung đường cao hạ từ M xuống CD nên
\(\frac{S_{CKM}}{S_{MCD}}=\frac{CK}{CD}=\frac{12}{24}=\frac{1}{2}\) mà BC=CD nên \(\frac{CK}{CD}=\frac{CK}{BC}=\frac{1}{2}\)
Cho hình vuông abcd trên BC lấy M sao cho BM bằng 2/3 BC
a )Tính diện tích ABM biết cạnh của hình vuông là 12 cm
b) kéo dài AM cắt cạnh D C tại K. So sánh CK và DK
Hình c tự vẽ nha
a) Diện tích ABM là: AB.AM/2=(12.12.2/3)/2=48 \(cm^2\)
b) Vẽ hình dễ thấy CK<DK
Cho hình vuông abcd cạnh a. trên cạnh bc lấy điểm m, trên cạnh cd lấy điểm n sao cho bm=cn. am và bn cắt nhau tại h. tính gtnn của mn theo a.
Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .
Đáp án A
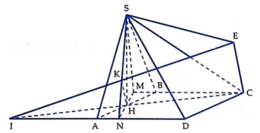
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2 3 a x 4 x 2 + 3 a 2 x 2 + 7 a 2
⇒ sin φ = 2 3 a x 4 x 4 + 21 a 4 + 31 a 2 x 2 ≤ 2 3 a x 4 21 a 2 x 2 + 31 a 2 x 2 = 2 3 4 21 + 31
Dấu “=” xảy ra khi và chỉ khi 4 x 4 = 21 a 4 ⇔ x 4 = 21 4 a 4 ⇔ x = 21 4 4 a .
Vậy góc φ đạt lớn nhất khi sin φ đạt lớn nhất, khi đó S H = 21 4 4 a
Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .