Bài 1:

Gọi hai số tự nhiên cần tìm là a,b

Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)

Tổng của hai số là 100 nên a+b=100(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)

Bài 2:

Gọi hai số cần tìm là a,b

Hiệu của hai số là 10 nên a-b=10(4)

Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)

Từ (3) và (4) ta có hệ phương trình:

\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)

Bài 3:

Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)

Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)

Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:

\(\overline{ab}+\overline{ba}=77\)

=>\(10a+b+10b+a=77\)

=>11a+11b=77

=>a+b=7(6)

Từ (5) và (6) ta có hệ phương trình:

\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)

Vậy: Số tự nhiên cần tìm là 16

tổng =63

ST3+ST2+ST1=63

ST1*6+ST1*2+ST1=63

=>ST1*9=63

ST1=7

ST2=14

ST3=42

                                   Tổng 3 số là : 

                                                       21 nhân 3 = 63      (D/v)

Vì số thứ ba gấp ba lần số thứ hai , số thứ hai gấp hai lần số thứ nhất =>số thứ ba gấp 4 lần số thứ nhất .

    Theo bài ra ta có sơ đồ :

    Số thứ nhất :  (  1 phần)    

 Số thứ hai  :      (2 phần)              tong 63 

Số thứ ba   :    (  4 phần )

     Nhìn vào sơ đồ ta thấy ; 

   Tổng số phần bằng nhau là :      1 +2 + 4 = 7 ( phan ) 

 Số thứ nhất là :  63 :  7 = 9 ( d/v )

 Số thứ hai là :     9  nhân 2 =18 (d/v )

Số thứ ba là : 63 - 9 - 18 =36 (d/v )

                           ​đáp số :số thứ nhất : 9 

                                       số thứ hai : 18

                                        số thứ ba :  36

số thứ ba là 42

Cho hàm số y= f(x) =4x^3-2x. CMR với mọi x thì f(x)= -f(x). Giúp mình với

Nguyễn Đức Anh ơi nếu bạn muốn hỏi thì bạn phải ấn vô "Gửi câu hỏi" chứ 

Đáp án D

Gọi hai số cần tìm là a,b

Theo đề, ta có:

a+b=50 và 3a=3(b+10)

=>a+b=50 và 3a-3b=30

=>a+b=50 và a-b=10

=>a=30; b=20

Đáp án A

Gọi số thứ nhất là a; a  ∈ N, số thứ hai là b; b  ∈  N Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:

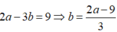
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:

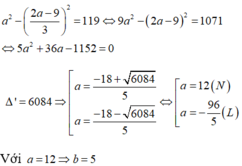
Vậy số lớn hơn là 12.

Đáp án A