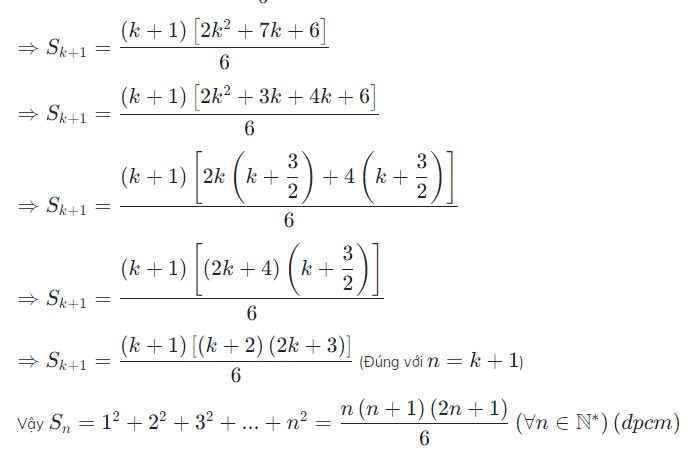chứng tỏ rằng với mọi n thuộc N* ta luôn có 1/n(n+1)=1/n-1/n+1

Những câu hỏi liên quan
chứng tỏ rằng với mọi n thuộc N ta luôn có
\(\dfrac{1}{1.6}+\dfrac{1}{6.11}+\dfrac{1}{11.16}+....+\dfrac{1}{\left(5n+1\right).\left(5n+6\right)}=\dfrac{n+1}{5n+6}\)
\(VT=\dfrac{1}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{\left(5n+1\right)\left(5n+6\right)}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-...+\dfrac{1}{5n+1}-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{5n+6-1}{5n+6}\)
\(=\dfrac{n+1}{5n+6}=VP\)
Đúng 2
Bình luận (0)
chứng minh rằng với mọi n thuộc N ta luôn có: 1/1.6+1/6.11+1/11.16+...+1/(5.n+1).(5.n+6)=n+1/5.n+6
Chứng tỏ rằng với mọi n E N ta luôn có :
a) n . ( n + 1 ) . ( n + 5 ) chia hết cho 3
b) n . ( 2n + 1 ) . ( 7n + 1 ) chia hết cho 6
Chứng minh rằng với mọi n thuộc N ta luôn có:
1/1.6 + 1/6.11 + 1/11.16 + ......+ 1/( 5n + 1) (5n + 6) = n+1/ 5n + 6
Chứng minh rằng với mọi n thuộc N ta luôn có : (x+1)^2n-x^2n-2x-1 chia hết cho x(x+1)(2x+1)
Chứng minh rằng với mọi số nguyên dương n , ta luôn có:
1/n+1 + 1/n+2 +...+ 1/2*n < 3/4
chứng minh rằng với mọi n thuộc N* ta luôn có:
\(\frac{1}{n+1}+\frac{1}{n+2}+\frac{1}{n+3}+...+\frac{1}{2n}<\frac{3}{4}\)
Chứng minh rằng với mọi số tự nhiên n khác 0 ta luôn có :
1² + 2² + 3² + .... + n² = n . (n+1).(2n+1)/6
Chứng tỏ rằng (n-1)n(n+1)chia hết cho 3 với mọi n thuộc Z
Vì n-1;n;n+1 là ba số nguyên liên tiếp
nên n(n-1)(n+1) chia hết cho 3!
=>n(n-1)(n+1) chia hết cho 3
Đúng 0
Bình luận (0)