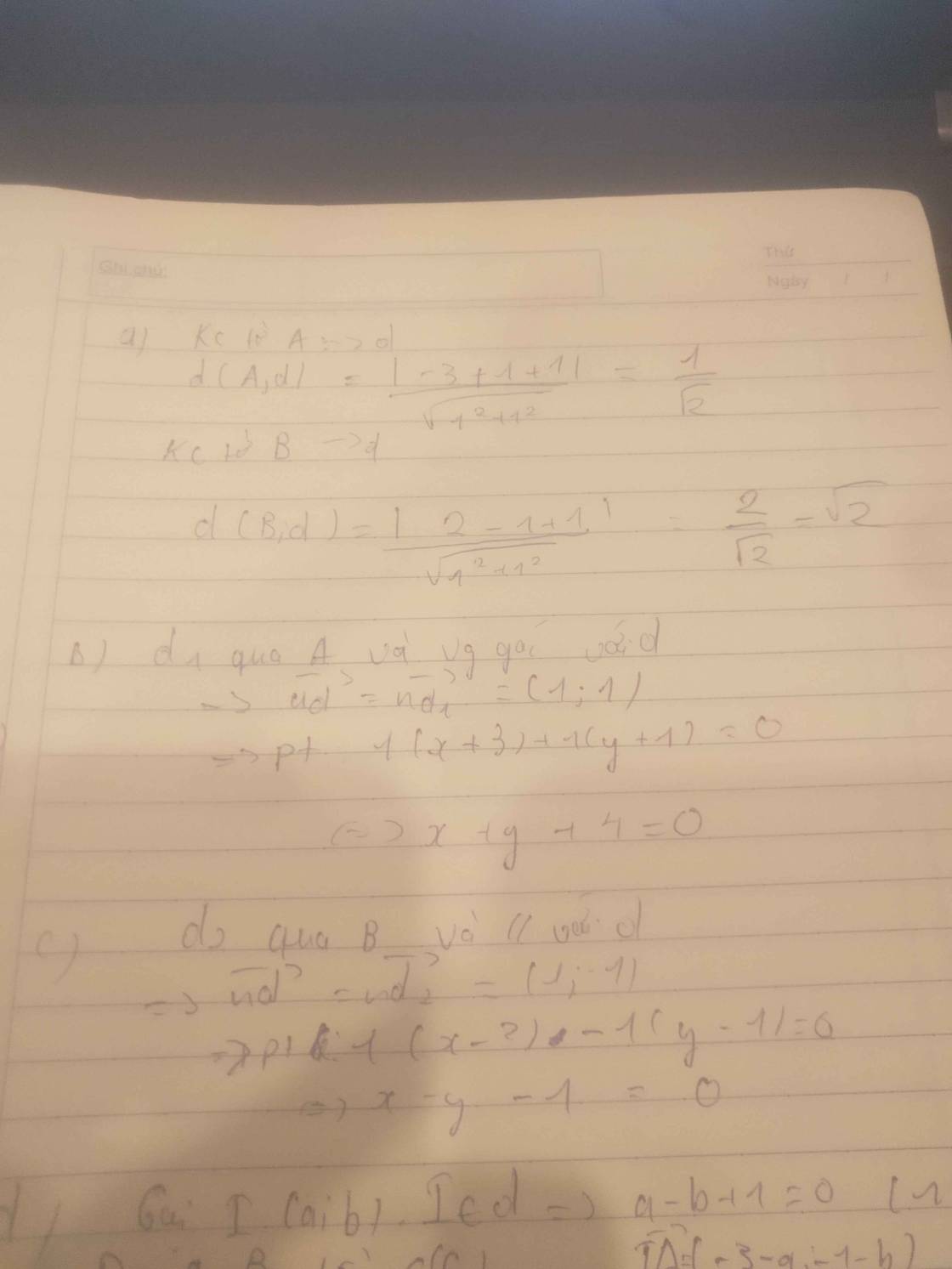viết pt đường thẳng (d) đi qua điểm B(0;m) và song song với đường thẳng x+2y=1

Những câu hỏi liên quan
Cho điểm A(-3;-1), B(2;1), đường thẳng d: x-y+1=0.
a. Tính khoảng cách từ A, B đến đường thẳng d.
b. Viết pt đường thẳng d1 đi qua A và vuông góc với d.
c. Viết phương trình đthẳng d2 đi qua B và song song với d.
d. Viết pt đường tròn (C) có tâm I thuộc d và đi qua 2 điểm A, B
Dạng 1 : Viết pt đưởng thẳng d (pt dạng tham số ,tổng quát ,chính tắc nếu có) đi qua 2 điểm A , B
Bài 1 : Viết pt đưởng thẳng d ( pt dạng tham số , tổng quát , chính tắc nếu có ) đi qua 2 điểm A , B biết A(2;1) , B(-4;5)
Dạng 2 : Viets pt đưởng thẳng d ( pt đoạn chẵn ) đi qua 2 điểm A(a;0) , B(0;b) , nằm trên các trục tọa độ với a,b≠0
BÀi 1 : viết pt đưởng thẳng ( pt đoạn chẵn ) đi qua 2 điểm A ,B biết A(3;0) , B(0;5)
Bài2 : viết pt đường thẳng d đi qua M và cùng với 2 trục tọa độ tạo thành...
Đọc tiếp
Dạng 1 : Viết pt đưởng thẳng d (pt dạng tham số ,tổng quát ,chính tắc nếu có) đi qua 2 điểm A , B
Bài 1 : Viết pt đưởng thẳng d ( pt dạng tham số , tổng quát , chính tắc nếu có ) đi qua 2 điểm A , B biết A(2;1) , B(-4;5)
Dạng 2 : Viets pt đưởng thẳng d ( pt đoạn chẵn ) đi qua 2 điểm A(a;0) , B(0;b) , nằm trên các trục tọa độ với a,b≠0
BÀi 1 : viết pt đưởng thẳng ( pt đoạn chẵn ) đi qua 2 điểm A ,B biết A(3;0) , B(0;5)
Bài2 : viết pt đường thẳng d đi qua M và cùng với 2 trục tọa độ tạo thành một tam giác có diện tích S cho trước biết M(-4;10) , SOAB =2
Bài 1:
\(\overrightarrow{AB}=\left(-6;-4\right)=\left(3;2\right)\)
Phương trình tham số AB là:
\(\left\{{}\begin{matrix}x=2+3t\\y=2+t\end{matrix}\right.\)
Phương trình tổng quát AB là:
-2(x-2)+3(y-1)=0
=>-2x+4+3y-3=0
=>-2x+3y+1=0
=>2x-3y-1=0
Đúng 0
Bình luận (0)
Cho A ( 1; 3 ), B( 4; -1 ), (d) x = 2y+1
a, Viết pt đường thẳng qua A, B
b, Viết pt đường thẳng đi qua A và cắt trục hoành tại điểm có tung độ = -1
c, Viết pt đường thẳng qua A và có hệ số góc là 5
d, Viết pt đường thẳng qua A song song với (d)
e, Viết pt đường thẳng qua A vuông góc với (d)
(d): 2y+1=x
=>2y=x-1
=>y=1/2x-1/2
a: Gọi (d1): y=ax+b là phương trình đường thẳng AB
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=3\\4a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=4\\a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{3}\\b=3-a=3+\dfrac{4}{3}=\dfrac{13}{3}\end{matrix}\right.\)
c: Gọi (d2): y=ax+b là phương trình đường thẳng cần tìm
Vì (d2) có hệ số góc là 5 nên a=5
Vậy: (d2): y=5x+b
Thay x=1 và y=3 vào (d2), ta được:
b+5=3
hay b=-2
d: Gọi (d3): y=ax+b là phương trình đường thẳng cần tìm
Vì (d3)//(d) nên a=-1/2
Vậy: (d3): y=-1/2x+b
Thay x=1 và y=3 vào (d3), ta được;
b-1/2=3
hay b=7/2
Đúng 0
Bình luận (0)
Viết PT đường thẳng d biêts (d) đi qua E(0 ; 4) và đồng quy với hai đường thẳng
b) (d'): y=2x - 3; (d"): y=7 - 3x tại một điểm
1. Cho điểm A\(\left(8;-1\right)\) và đường thẳng d: \(2x-y-7=0\). Viết pt đt d đi qua O sao cho khoảng cách từ A đến đường thẳng d lớn nhất .
2. Cho điẻm M (3;1) .Viết pt đt Δ đi qua M ,cắt tia Ox và tia Oy tương ứng tại A và B ( khác O ) sao cho :
a) \(P=\dfrac{9}{OA^2}+\dfrac{4}{OB^2}\) nhỏ nhất
Viết pt tổng quát của đường thẳng d
a) Đi qua điểm M(-2;-5) và song song với đường phân giác góc phần tư thứ nhất
b) Đi qua điểm M(3;-1) và vuông góc với đường phân giác góc phần tư thứ hai
c) Viết pt tham số của đg thẳng d đi qua điểm M(-4;0) và vuông góc với đường phân giác thứ hai
a, Đường phân giác góc phần tư thứ nhất là một nửa đường thẳng x - y = 0 nằm ở góc phần tư thứ nhất
=> d nhận (1 ; -1) làm vecto pháp tuyến
=> PT đi qua M (-2 ; -5) là
x + 2 - y - 5 = 0 ⇔ x - y - 3 = 0
b, c, Lười lắm ko làm đâu :)
Đúng 2
Bình luận (1)
Cho đường thẳng d : -3x+y-1=0 và điểm I(-2;4).
a. Viết pt đường thẳng d1 đối xứng với đường thẳng d2 : 2x+y=0 qua d
b. Viết pt đường thẳng d3 sao cho khoảng cách giữa d và d3 bằng 6
Viết PT tham số của đường thẳng D đi qua điểm A(-1;2) và vuông góc vs đường thẳng △: 2x-y+4=0
Đường thẳng \(\Delta\) có 1 vtpt là \(\left(2;-1\right)\)
Do \(d\perp\Delta\) nên d nhận \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=-1+2t\\y=2-t\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho ∆ABC cân tại A biết cạnh bên AB : 3x-y+5=0 và cạnh đáy x+y-1=0
a,viết pt cạnh AC biết đường thẳng AC đi qua điểm M (1,-3)
b,viết pt đường cao của ∆ABC
c,viết pt đường trung tuyến của ∆ABC
d, viết pt đường phân giác trong của ∆ABC