1. Cho tam giác ABC vuông tại A. tia phân giác góc B cắt AC tại D. từ A kẻ AE vuông góc BD tại E và cắt BC tại M
A. chứng minh tam giác ABC bằng tam giác MBE
B. chứng minh DM vuông góc với BC
C .Kẻ AH vuông góc với BC tại I. Chứng minh AM là tia phân giác của góc IAC
câu 2: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ tia phân giác AD của góc A (D thuộc BC)
A. chứng minh tam giác ABD bằng tam giác ACD
B. Vẽ đường trung tuyến của tam giác ABC cắt cạnh AC tại G. chứng minh G là trọng tâm của tam giác ABC
C. Gọi H là trung điểm của cạnh DC. qua h Vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh tam giác DEC cân
D. Chứng minh ba điểm B, G, E thẳng hàng
Câu 3 Cho tam giác ABC vuông tại A. Vẽ trung tuyến AM của tam giác ABC, Kẻ MH vuông góc với AC. Trên tia đối của tia MH đặt điểm K sao cho MK bằng MH
a. chứng minh tam giác MHC bằng tam giác MKB và BK vuông góc với KH
B. Chứng minh AB song song với HK và BK = AH.
C. Vẽ BH cắt AB tại g. Gọi I là trung điểm của AB. Chứng minh ba điểm C, G, I thẳng hàng
câu4 Cho tam giác ABC vuông tại A. gọi M là trung điểm cạnh BC. trên tia đối của tia MA lấy điểm D sao cho MD = MA.
A . chứng minh tam giác MCD bằng tam giác MBD và AC song song với BD
B. Gọi I là trung điểm AM, J là trung điểm BM. AJ cắt BI tại G. Chứng minh tam giác GAB là tam giác cân
Câu 5 cho tam giác ABC vuông tại A (AB bé hơn AC). vẽ BD là tia phân giác của góc ABC (D thuộc AC). trên đoạn BC lấy điểm E sao cho BE bằng BA
a chứng minh tam giác ABD bằng tam giác EBD .Từ đó suy ra góc BED là góc vuông
b. tia ED cắt tia BA tại EF. Chứng minh tam giác BED cân
C. Chứng minh tam giác AFC bằng tam giác ECF
D.Chứng minh: AB + AC >DE+BC
câu 6: Cho tam giác ABC vuông tại A. Vẽ đường phân phân giác BD của tam giác ABC và E là hình chiếu của D trên BC
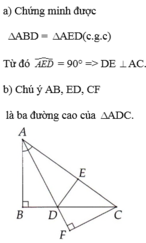
a. chứng minh tam giác ABD bằng tam giác EBD và AE vuông góc với BD
B. Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh tam giác ABC bằng tam giác AFC
C. Qua A vẽ đường thẳng vuông góc với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng
câu 7: Cho tam giác ABC cân tại A (góc A bé hơn 90 độ). vẽ AD là phân giác của góc A (D thuộc BC)
A . Chứng minh tam giác ABD bằng tam giác ACD
B. lấy H là trung điểm của AB. Trên tia đối của tia HC lấy điểm K sao cho HK = HC. Chứng minh rằng AK = BC
c. CH cắt AD tại G. Chứng minh (BA+BC)÷6 >GH