giải các pt và biểu diễn trục số
2x-8>4
giải các pt và biểu diễn trục số
2x-8<4-2x
`2x-8<4-2x`
`<=> 2x+2x < 4+8`
`<=> 4x < 12`
`<=> x<3`
Vậy bpt có tập nghiệm \(S=\left\{x|x< 3\right\}\)
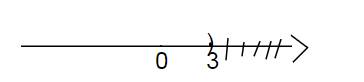
giải các pt và biểu diễn trục số
5x+4≥ -11 +2x
\(5x+4\ge-11+2x\)
\(\Leftrightarrow5x-2x\ge-11-4\)
\(\Leftrightarrow3x\ge-15\)
\(\Leftrightarrow x\ge-5\)
Vậy bất phương trình có nghiệm là: \(S=\left\{xIx\ge-5\right\}\)
Biểu diễn
Giải pt và biểu diễn tập nghiệm trên trục số x - 17 < 19 -2x
\(x-17< 19-2x\)
\(\Leftrightarrow x+2x< 19+17\)
\(\Leftrightarrow3x< 36\)
\(\Leftrightarrow x< 12\)
Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số. 4x – 8 ≥ 3(3x – 2) + 4 – 2x
Ta có: 4x – 8 ≥ 3(3x – 2) + 4 – 2x
⇔ 4x – 8 ≥ 9x – 6 + 4 – 2x
⇔ 4x – 9x + 2x ≥ - 6 + 4 + 8
⇔ -3x ≥ 6
⇔ x ≤ -2
Vậy tập nghiệm của bất phương trình là {x|x ≤ -2}
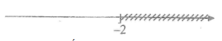
giải các pt và biểu diễn trục số
3x+9>0
\(3x+9>0\)
\(\Leftrightarrow3x>-9\)
\(\Leftrightarrow x>-2\)
Vậy bất phương trình có nghiệm là:\(S+\left\{xIx>-2\right\}\)
Biểu diễn
giải các pt và biểu diễn trục số
-5x+1≥3x+3
\(-5x+1\ge3x+3\)
\(\Leftrightarrow-5x-3x\ge3-1\)
\(\Leftrightarrow-8x\ge2\)
\(\Leftrightarrow x\le-\dfrac{1}{4}\)
Vậy bất phương trình có tập nghiệm là:\(S=\left\{x|x\le-\dfrac{1}{4}\right\}\)
Biểu diễn
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
a) 4 x − 3 < − 8 + 5 x ;
b) x + 2 2 − 2 x + 3 x − 4 > x 3 − x
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số 2x – 4 < 0
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
\(\dfrac{1-2x}{4}-2< \dfrac{1-5x}{8}\)
\(\dfrac{1-2x}{4}-2< \dfrac{1-5x}{8}\)
\(\Leftrightarrow\dfrac{2\left(1-2x\right)-16}{8}< \dfrac{1-5x}{8}\)
\(\Leftrightarrow2\left(1-2x\right)-16< 1-5x\)
\(\Leftrightarrow2-4x-16< 1-5x\)
\(\Leftrightarrow x< 15\)
Vậy \(S=\left\{x|x< 15\right\}\)