a) \(\frac{\left(24-3\right).24}{2}=252\)đường chéo

b) \(\left(n-3\right).n=340\)

\(n^2-3n=340\)

\(n^2-3n-340=0\)

\(n^2-20n+17n-340=0\)

\(n\left(n-20\right)+17\left(n-20\right)\)

\(\left(n+17\right)\left(n-20\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}n+17=0\\n-20=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}n=-17\\n=20\end{cases}}\)

n = -17 ( loại )

n = 20 ( nhận )

Vậy n = 20 hay số cạnh của đa giác là 20 

1 Đa giác có n cạnh có : 

- Số đường chéo từ 1 đỉnh là : (n - 3) 
- Số đỉnh là n 

Do 1 đường chéo nối 2 đỉnh 
=> 1 Đa giác có n cạnh có n(n - 3)/2 đường chéo 

biết tổng số đường chéo là 170 

=> n(n - 3)/2 = 170 

=> n² - 3n - 340 = 0 

∆ = (-3)² - 4.(-340) = 1369 

=> √∆ = 37 

=> n = ... (tự giải)

b) Đa giác có n cạnh có : 

- Số đường chéo từ 1 đỉnh là : (n - 3) 
- Số đỉnh là n 

Do 1 đường chéo nối 2 đỉnh 
=> 1 Đa giác có n cạnh có n \(\frac{\left(n+3\right)}{2}\)đường chéo

Biết tổng số đường chéo là 170 

\(\Rightarrow\frac{n\left(n-3\right)}{2}=170\)

\(\Rightarrow n^2-3-340=0\)

\(\Delta=\left(-3\right)^2-4.\left(-340\right)=1369\)

\(\sqrt{\Delta}=37\)

\(\Rightarrow n=37\)

Chọn B

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )

Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n  ⇔ n 2 - 3 n - 2 n = 0

⇔ n 2 - 5 n = 0 ⇔ n ( n - 5 ) = 0  ⇔ 

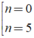
So sánh điều kiện ta có n = 5 thỏa mãn.

Chọn A

144 độ

Bài của bạn có thể tổng quát hoá như sau:
Chứng minh rằng trong mọi đa giác lồi với số cạnh chẵn, tồn tại đường chéo không song song với một cạnh nào của đa giác.
Solution:
Nhận xét rằng nếu 1 đa giác có nn cạnh thì có n(n−3)2n(n−3)2 đường chéo.
Xét 1 đa giác lồi bất kì với số cạnh chẵn (đa giác lồi 2k2k cạnh và k≥2k≥2, ở đây của bạn là 16).
AD nhận xét, khi đó số đường chéo của đa giác là: g=k(2k−3)=2k(k−2)+kg=k(2k−3)=2k(k−2)+k, suy ra:
g>2k(k−2)g>2k(k−2) (1).
Giả sử trái lại đa giác này có tính chất : Mỗi đường chéo của nó đều song song với một cạnh nào đó của đa giác. Đa giác này có 2k2k cạnh, vì thế từ (1) suy ra tồn tại ít nhất k−1k−1 đường chéo d1,d2,…,dk−1d1,d2,…,dk−1 mà các đường chéo này cùng song song với một cạnh aa nào đó của tam giác đã cho. Thật vậy, nếu ngược lại mỗi cạnh tối đa là song song k−2k−2 đường chéo, thế thì tối đa ta chỉ có (k−2)2k(k−2)2k đường chéo và g≥2k(k−2)g≥2k(k−2). Điều này mâu thuẫn với (1).
Như thế ta có kk đường thẳng song song với nhau là: d1,d2,…,dk−1,ad1,d2,…,dk−1,a.
Lại có đa giác đã cho là đa giác lồi, nên các đường chéo d1,d2,…,dk−1d1,d2,…,dk−1 cùng nằm trên 1 nửa mặt phẳng bờ XĐ cạnh aa.
Không giảm tổng quát có thể cho d1d1 là đường chéo xa nhất đối với aa (vì nếu không thì đánh số lại các đường chéo trên). Ta có tất cả kk đoạn thẳng phân biệt, nên mỗi đỉnh của đa giác đều là đầu mút của một đoạn nào đó trong số kk đoạn trên. Từ đó suy ra toàn bộ đa giác nằm hẳn về một ửa mặt phẳng xác định bởi d1d1. Do d1d1 là đường chéo, nên điều này mâu thuẫn với tính lồi của đa giác. Vậy giả thiết phản chứng là sai.
Ta có điều phải chứng minh. 

Solution:
Nhận xét rằng nếu 1 đa giác có n cạnh thì có n(n−3)2 đường chéo.
Xét 1 đa giác lồi bất kì với số cạnh chẵn (đa giác lồi 2k cạnh và k≥2, ở đây của bạn là 16).
AD nhận xét, khi đó số đường chéo của đa giác là: g=k(2k−3)=2k(k−2)+k, suy ra:
g>2k(k−2) (1).
Giả sử trái lại đa giác này có tính chất : Mỗi đường chéo của nó đều song song với một cạnh nào đó của đa giác. Đa giác này có 2k cạnh, vì thế từ (1) suy ra tồn tại ít nhất k−1 đường chéo d1,d2,…,dk−1 mà các đường chéo này cùng song song với một cạnh a nào đó của tam giác đã cho. Thật vậy, nếu ngược lại mỗi cạnh tối đa là song song k−2 đường chéo, thế thì tối đa ta chỉ có (k−2)2k đường chéo và g≥2k(k−2). Điều này mâu thuẫn với (1).
Như thế ta có k đường thẳng song song với nhau là: d1,d2,…,dk−1,a.
Lại có đa giác đã cho là đa giác lồi, nên các đường chéo d1,d2,…,dk−1 cùng nằm trên 1 nửa mặt phẳng bờ XĐ cạnh a.
Không giảm tổng quát có thể cho d1 là đường chéo xa nhất đối với a (vì nếu không thì đánh số lại các đường chéo trên). Ta có tất cả k đoạn thẳng phân biệt, nên mỗi đỉnh của đa giác đều là đầu mút của một đoạn nào đó trong số k đoạn trên. Từ đó suy ra toàn bộ đa giác nằm hẳn về một ửa mặt phẳng xác định bởi d1. Do d1 là đường chéo, nên điều này mâu thuẫn với tính lồi của đa giác. Vậy giả thiết phản chứng là sai.
Ta có điều phải chứng minh.

Bài của bạn có thể tổng quát hoá như sau:
Chứng minh rằng trong mọi đa giác lồi với số cạnh chẵn, tồn tại đường chéo không song song với một cạnh nào của đa giác.
Solution:
Nhận xét rằng nếu 1 đa giác có nn cạnh thì có n(n−3)2n(n−3)2 đường chéo.
Xét 1 đa giác lồi bất kì với số cạnh chẵn (đa giác lồi 2k2k cạnh và k≥2k≥2, ở đây của bạn là 16).
AD nhận xét, khi đó số đường chéo của đa giác là: g=k(2k−3)=2k(k−2)+kg=k(2k−3)=2k(k−2)+k, suy ra:
g>2k(k−2)g>2k(k−2) (1).
Giả sử trái lại đa giác này có tính chất : Mỗi đường chéo của nó đều song song với một cạnh nào đó của đa giác. Đa giác này có 2k2k cạnh, vì thế từ (1) suy ra tồn tại ít nhất k−1k−1 đường chéo d1,d2,…,dk−1d1,d2,…,dk−1 mà các đường chéo này cùng song song với một cạnh aa nào đó của tam giác đã cho. Thật vậy, nếu ngược lại mỗi cạnh tối đa là song song k−2k−2 đường chéo, thế thì tối đa ta chỉ có (k−2)2k(k−2)2k đường chéo và g≥2k(k−2)g≥2k(k−2). Điều này mâu thuẫn với (1).
Như thế ta có kk đường thẳng song song với nhau là: d1,d2,…,dk−1,ad1,d2,…,dk−1,a.
Lại có đa giác đã cho là đa giác lồi, nên các đường chéo d1,d2,…,dk−1d1,d2,…,dk−1 cùng nằm trên 1 nửa mặt phẳng bờ XĐ cạnh aa.
Không giảm tổng quát có thể cho d1d1 là đường chéo xa nhất đối với aa (vì nếu không thì đánh số lại các đường chéo trên). Ta có tất cả kk đoạn thẳng phân biệt, nên mỗi đỉnh của đa giác đều là đầu mút của một đoạn nào đó trong số kk đoạn trên. Từ đó suy ra toàn bộ đa giác nằm hẳn về một ửa mặt phẳng xác định bởi d1d1. Do d1d1 là đường chéo, nên điều này mâu thuẫn với tính lồi của đa giác. Vậy giả thiết phản chứng là sai.
Ta có điều phải chứng minh.