Question

Một đa giác có số đường chéo bằng số cạnh của đa giác thì đa giác có số cạnh là? 

A. 5.   

B. 6. 

C. 4.   

D. 7. 

Answer 1

Số đường chéo của đa giác n cạnh là (n( n - 3 ))/2. ( n ∈ N, n ≥ 3 )

Theo giả thiết ta có (n( n - 3 ))/2 = n ⇔ n( n - 3 ) = 2n  ⇔ n 2 - 3 n - 2 n = 0

⇔ n 2 - 5 n = 0 ⇔ n ( n - 5 ) = 0  ⇔ 

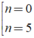
So sánh điều kiện ta có n = 5 thỏa mãn.

Chọn A